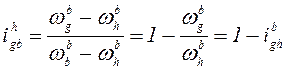Волновые зубчатые передачи. Принцип работы. Кинематика передачи. Основные схемы. Оценка и применение, страница 2

,                              (21.2)

откуда передаточное отношение волновой передачи с ведомым гибким колесом:

.                                                   (21.3)

          Передаточное отношение передачи при ведущем волновом генераторе с использованием формулы Виллиса:

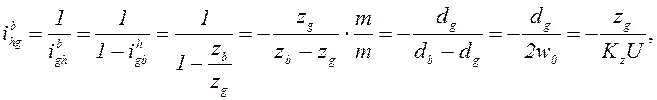          (21.4)

   где U – число волн деформирования (U = 1; 2; 3);

          K_z – коэффициент кратности (K_z = 1; 2; 3).

Знак минус свидетельствует о противоположном направлении вращения гибкого колеса g и волнового генератора h. В волновой передаче, таким образом, передаточное отношение определяется не отношением диаметров, как в простой зубчатой передаче, а отношением диаметра ведомого колеса к разности диаметров (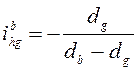) либо отношением числа зубьев ведомого колеса к разности чисел зубьев (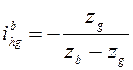) или к числу волн ().

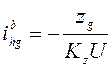          Также по методу Виллиса определяют передаточное отношение волновой передачи с ведомым жёстким колесом и неподвижным гибким (рис. 21.5):

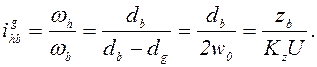                                    (21.5)

          В формуле (21.5) знак передаточного отношения “плюс”, следовательно, жёсткое колесо и волновой генератор вращаются в одном направлении.

Рис. 21.5. Волновая передача с неподвижным гибким колесом

          Пример 21.1. Рассчитать передаточное отношение волновых передач по двум вариантам: а) закреплено жёсткое колесо; б) закреплено гибкое колесо. Исходные данные:  число зубьев жёсткого колеса z_b = 202, число зубьев гибкого колеса z_g = 200,  число волн U = 2.

          Решение:

Передаточное отношение по варианту а:   

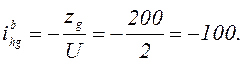
Передаточное отношение по варианту б:

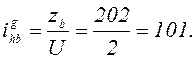
Выводы. 1. Передаточные отношения в обоих вариантах отличаются незначительно.

2. При закреплении жёсткого колеса гибкое вращается против направления вращения волнового генератора.

3. При закреплении гибкого колеса жёсткое вращается по направлению вращения волнового генератора.

4. Передаточное число существенно отличается от передаточных отношений и незначительно превышает единицу (u = z_b/ z_g = 202/200 = 1,01).

NB 21.2. Волновой принцип передачи движения обеспечивает высокое передаточное отношение в одной ступени.

Из формулы 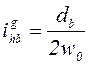 видно, что чем больше величина деформации гибкого элемента, тем меньше передаточное отношение, но при больших  гибкое колесо может оказаться недостаточно прочным. Таким образом, минимальное передаточное отношение ограничивают по условиям прочности гибкого колеса. Для колёс из высокопрочных сталей минимальное передаточное отношение i_min = ± 70.

          При больших передаточных отношениях зубья колес мелкие и могут проскакивать друг относительно друга. Поэтому максимальное передаточное отношение i_max = ± 300. Однако в кинематических передачах i может составлять несколько десятков тысяч.

21.3. Основные схемы

          Кроме рассмотренных схем наибольший интерес представляет схема на рис. 21.6 – герметичная передача, которая передает движение через герметичную стенку, разделяющую пространства А и Б. Гибкий стакан герметично прикрепляют к стенке, например, приваривают. Зубчатый венец располагают в средней части стакана. Такая передача находит применение в химической, атомной, космической и других областях техники.

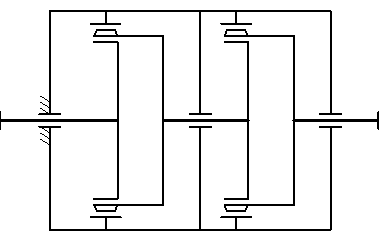
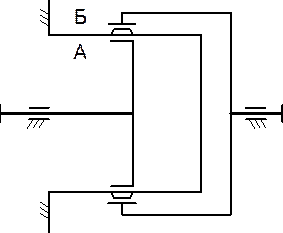
  Рис. 21.6. Передача вращения                   Рис. 21.7. Двухступенчатая волновая

в герметизированное пространство                                      передача

          При необходимости увеличить передаточное отношение используется двухступенчатая волновая передача (рис. 21.7). На рис. 21.8 приведена схема волновой передачи механизма поворота башенного крана КБ–60. В передаче развивается мощность Р = 2,2 кВт и момент Т = 630 Н×м при передаточном отношении  и КПД h = 0,86. На рис. 21.9 представлена схема волновой передачи, встроенной в барабан грузовой лебёдки самоходного крана с гидроприводом: Р = 20 кВт, Т = 12000 Н×м, , h = 0,86.

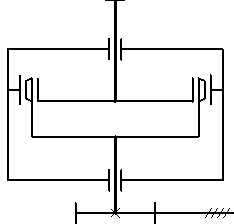
             Рис. 21.8. Механизм поворота                Рис. 21.9. Передача, встроенная

                                                                                              в барабан лебёдки

          Встречаются также схемы с электромагнитным и гидравлическим генераторами волн и винтовая волновая передача.

21.4. Оценка и применение

          Достоинства:

          1. Большое передаточное отношение в одной ступени.

          2. Высокая нагрузочная способность при малых габаритах и массе (масса в 2 раза меньше, чем у планетарных редукторов).

          3. Высокая кинематическая точность.

          4. Высокий КПД, сопоставимый с КПД планетарных передач.

          5. Малые нагрузки на валы и опоры.