Проверка гипотезы о распределении случайных величин, страница 2

Этот вопрос можно понимать следующим образом. Пусть случайная величина X распределена по закону f(t); тогда событие, состоящее в том, что результаты n испытаний окажутся распределенными по интервалам D₁, D₂ ... D_m с помощью чисел k₁, k₂ ....k_m  имеет некоторую вероятность, зависящую в первую очередь от гипотетического распределения f(t). Если эта вероятность окажется близкой к единице, то есть основания принять гипотезу о данном распределении случайной величины.

Уточним задачу статистической проверки гипотезы о распределении.

Каждому интервалу (классу) D_i соответствует теоретическая вероятность p_i того, что случайная величина X примет значение из этого класса

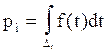,                                                                                                  (12)

а также относительная частота наступления этого события в результате n испытаний или эмпирическая вероятность

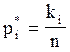.                                                                                                          (13)

Если гипотеза о распределении справедлива, то отклонения  должны быть малы.

Для выполнения, описанной в общих чертах проверки гипотезы необходимо уметь вычислять вероятность того или иного отклонения набора теоретических частот от набора эмпирических частот.

Существуют функции, распределение которых не зависит не от гипотетического распределения f(t) ни от количества испытаний, если только n велико.

Одна из самых широко используемых функций это функция c² (хи-квадрат):

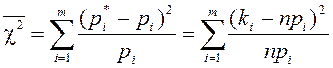                                                      (14)

Как установлено американским математиком К. Пирсоном случайная величина c² распределена по следующему дифференциальному закону:

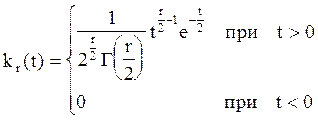                                                         (15)

Здесь Г - гамма функция:

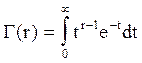                                                                                            (16)

В случае хорошего совпадения теоретических и эмпирических данных величина c² не будет принимать слишком больших значений. Поэтому вероятности P(c² >t) в случае хорошего совпадения должны быть малы при больших  t.

При проверке гипотезы с использованием  c² критерия Пирсона используют два способа:

1 Задают некоторую малую вероятность e и находят такое t_e, что P(c²>t_e)= e. Значение P(c²> t_e) можно определить как

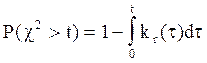 = e.                                                                        (17)

При этом естественно считать, что если полученное из опыта значение будет больше, чем t_e, то гипотезу следует считать противоречащей опытным данным. Говорят, что гипотеза несостоятельна на уровне значимости e.

2 Вычисляют значение , затем определяют вероятность того, что случайная величина c² превзойдет значение . Если вероятность такого события велика (это значит, что  мало), то гипотеза принимается. Можно говорить, что гипотеза состоятельна на уровне значимости

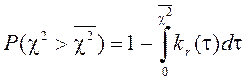.                                                                      (18)

Параметр r (число степеней свободы) определяется как

r = m - s.                                                                                                          (19)

s -  количество связей, налагаемых на эмпирические частоты (вероятности) .

Примеры связей:

1

2

3

При проверке гипотезы о равномерном распределении используют связь 1, при этом s=1. При проверке гипотезы о нормальном распределении используют связи 1,2 и 3 , при этом s=3.

2 Задание на лабораторную работу

Для каждой из двух случайных величин  X1 и X2, представленных выборками, по критерию Пирсона проверить гипотезу о равномерном и нормальном законе их распределения по второму способу.

Порядок выполнения работы:

1 Из исходного статистического материала для случайной величины X1 получить статистический ряд, с количеством классов равным 8. Вычислить величины классов . По формулам (12) и (13) вычислить эмпирические и теоретические вероятности (и ) того что случайная величина примет значение, принадлежащее данному классу. Результат оформить в виде таблицы 2, дополнив последнюю строкой для эмпирических частот (вероятностей).

2 Вычислить выборочное среднее арифметическое и выборочную дисперсию.

2 По формуле (14) вычислить значение . Используя формулы (3, 15, 16) вычислить вероятность, того, что случайная величина c² превзойдет значение .

3. Повторить пункты 1 и 2 для случайной величины X2

4. Сделать выводы.

Примечания:

1 Численное интегрирование производить по методу трапеций.

2 При численном интегрировании для нахождения теоретических частот и значения 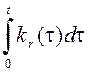 рекомендуется разбить интервал интегрирования на 1000 участков.

3 При численном интегрировании для нахождения значения гамма функции величину шага рекомендуется принять 0.1. Интегрирование можно считать завершенным, если приращение искомого значения гамма-функции после очередного шага меньше 10^-6.