Проверка гипотезы о распределении случайных величин

Проверка гипотезы о распределении случайных величин

1 Общие сведения о распределении случайных величин.

Случайная величина - величина, значение которой невозможно предсказать до момента проведения опыта.

Распределением дискретной случайной величины называется функция, сопоставляющая каждому значению x_i случайной величины X ее вероятность p_i.

                                                                                                         (1)

Распределение дискретной случайной величины удобно представить таблицей:

Таблица 1.

x1	x2	...	xn
p1	p2	...	pn

Для непрерывной случайной величины удобно группировать полученные в результате испытаний значения в классы, за величину которых принимают их середину (статистический ряд):

Таблица 2.

		...
p1	p2	...	pn

Распределение полностью характеризует случайную величину, указывая возможные значения и вероятности с которыми эти значения появляются в результате испытаний.

Рассматривают два вида распределения непрерывной случайной величины: интегральное и дифференциальное.

Интегральной функцией распределения непрерывной случайной величины X называется функция переменной t, выражающая вероятность того, что случайная величина в результате испытания примет значение меньше, чем t.

Если вероятность того, что случайная величина X примет значение меньше, чем t обозначить P(X<t), то интегральная функция распределения F(t) переменной t, определяется равенством:

F(t)=P(X<t)                                                                                                     (2)

или

1-F(t)=P(X>t)                                                                                                  (3)

 

Рисунок 1.

Вероятность того, что случайная величина примет значение от t₁ до t₂ можно определить по формуле:

F(t₂)-F(t₁)=P(t₁<X<t₂)                                                                                    (4)

Производная интегральной функции распределения случайной величины называется дифференциальной функцией  (дифференциальным законом ) распределения случайной величины.

F’(t)=f(t)                                                                                                         (5)

Значения функции f(t) называются плотностью вероятности случайной величины.

P(t<X<t+Dt)»f(t) Dt                                                                                        (6)

Рассмотрим два наиболее часто встречающихся распределения.

1 Нормальное распределение

Распределение непрерывной случайной величины X, заданное дифференциальной функцией распределения

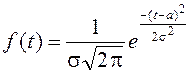                                                                                   (7)

называется нормальным распределением.

 

Рисунок 2.

Величина «а» характеризует сдвиг (математическое ожидание), а «s» степень «растяжения» по оси абсцисс (среднеквадратическое отклонение).

Интегральное распределение удобно выражать через интеграл вероятностей:

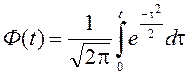                                                                                   (8)

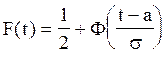                                                                                       (9)

2 Распределение непрерывной случайной величины, заданное дифференциальной функцией распределения

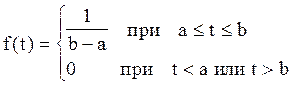                                                              (10)

 

Рисунок 3.

Интегральный закон равномерного распределения:

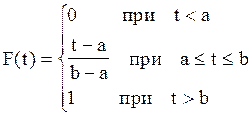                                                                      (11)

Практическое изучение какой либо случайной величины часто происходит в следующих обстоятельствах: закон распределения и характеристики случайной величины неизвестны, однако известны результаты некоторого количества испытаний этой случайной величины.

Нахождение функции распределения случайной величины требует очень большого объема статистического материала. Поэтому эту задачу часто упрощают и сводят к ответу на вопрос: верно или нет, что данная случайная величина распределена по конкретному закону. Такая постановка задачи и носит название «статистическая проверка гипотез».

Пусть проведено n испытаний случайной величины X, в результате которой получены ее значения x₁, x₂ ... x_n.

Пусть а=min(x_i), b=max(x_i). Разделим интервал [a,b] на  m равных частей (классов) D₁, D₂ ... D_m. Пусть k₁, k₂ ....k_m количество элементов, попавший в интервал D₁, D₂ ... D_m соответственно.

Поставим следующий вопрос: насколько вероятно предположение о том, что данная случайная величина распределена по данному дифференциальному закону f(t).