




А=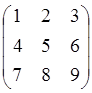 =
=![]()
![]()
Разложение определителя по элементам строки или столбца.
Дана квадратная матрица:
А=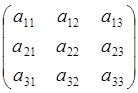
Минором ![]() , соответствующему
элементу
, соответствующему
элементу ![]() называется определитель матрицы,
полученный из данной вычеркиванием i строки и j столбца.
называется определитель матрицы,
полученный из данной вычеркиванием i строки и j столбца.
Например:
![]()
![]()
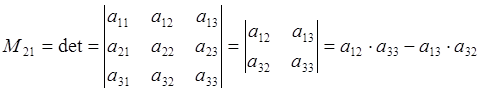
Алгебраическим
дополнением ![]() называется величина, определяемая
формулой:
называется величина, определяемая
формулой:
![]()
С учетом этих понятий можно доказать, что определитель любого порядка можно разложить по элементам, т.е. представить в виде:
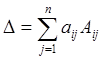
С учетом этого правили можно вычислить определитель любого порядка:
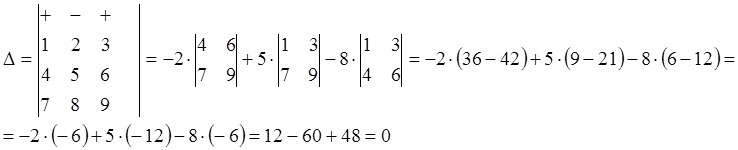
Свойства определителей.
ü 1) определитель равен нулю, если а) элементы какой-либо строки или столбца равны нулю;
б) элементы одной строки равны или пропорциональны элементам другой строки (столбцы аналогично);
ü 2) определитель не изменится, если к элементам строки (столбца) прибавить элементы строки (столбца), умноженного на число;
ü 3) если элементы строки (столбца) умножить на одно и тоже число, то определитель умножается на это же число;
ü 4) при перестановки местами двух соседних строк (столбцов) знак определителя меняется на противоположный;
ü
5) ![]() ;
;
ü
6) определитель произведения А![]() В равен произведению определителей (
В равен произведению определителей (![]() ;
;
ü
7) ![]() ;
;
ü
8) 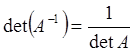 .
.
Общее правило вычисления определителей. Перестановки и их свойства.
Пусть даны 3 элемента, их можно расставить следующими способами:
![]()
![]()
![]() 3
3
![]()
![]() 1 2 3
- 0-я перестановка
1 2
1 2 3
- 0-я перестановка
1 2
3
![]()
![]()
![]() 2 1 3 - 1-я перестановка
1 2
2 1 3 - 1-я перестановка
1 2
![]()
![]()
![]() 3
3
![]() 2 3 1 - 2-я перестановка 1 2
2 3 1 - 2-я перестановка 1 2
![]()
![]()
![]()
![]() 3
3
3 2 1 - 3-я перестановка 1 2
![]()
![]()
![]() 3
3
![]() 3 1 2 - 4-я перестановка 1 2
3 1 2 - 4-я перестановка 1 2
![]() 3
3
![]()
![]()
![]()
1 3 2 - 5-я перестановка 1 2
![]()
![]()
![]() 3
3
1 2 3 - 6=0-я перестановка 1 2
Общее
количество перестановок из n элементов: ![]() !
!
Для учета четности или нечетности перестановок используется символ ε – антисимметричный символ Леви-Чивита.
Каждое из чисел ![]() принимает значение от 1 до n
принимает значение от 1 до n
0, если любые два индекса повторяются
ε= +1, если верхний индекс составляет четную перестановку нижних
-1 , если нечетная перестановка
Даны два вектора:
![]()
![]()
![]()
![]()
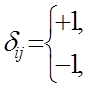 если і=j
если і=j
- символ Кронекера если і≠j
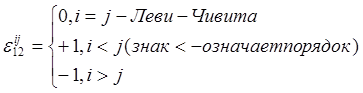
При записи формул используется правило суммирования по повторному индексу (правило Энштейна).
Справедливо равенство:
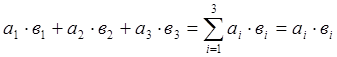 -
у двух сомножителей индексы совпадают, значит, по этому индексу ведется
суммирование от і=1 до і=n
-
у двух сомножителей индексы совпадают, значит, по этому индексу ведется
суммирование от і=1 до і=n
С учетом этого:
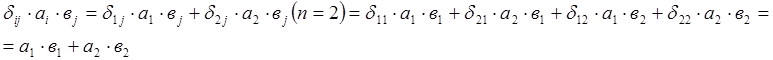
![]()
![]()
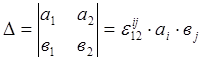
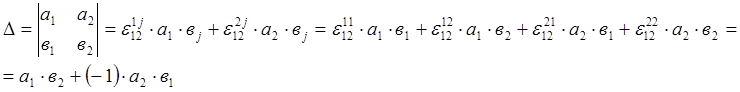
С учетом символа Леви-Чивита общее определение определителя имеет вид:
![]()
Р(n)=n! – общее количество перестановок.
Элементы линейной алгебры.
Множество А каких-то элементов называется линейным векторным пространством (линеал), если для его элементов определяются операции сложения и умножения на число (действительное или комплексное), обладающее свойствами:
ü
1) ![]() ;
;
ü
2) ![]() ;
;
ü
3) ![]() ;
;
ü
4) ![]() ;
;
ü
5) ![]() ;
;
ü
6) ![]() ;
;
ü
7) ![]() ;
;
ü
8) ![]() ;
;
ü
9) указывает размерность
пространства А - ![]() (аксиома размерности).
(аксиома размерности).
Аксиома размерности: указывает количество базисных векторов.
Элементы этого пространства называются векторами. Хотя реальными элементами могут быть:
1) векторы в обычном понимании;
2) матрицы одинаковых размеров;
3) многочлены одинаковых степеней и т.д.
Линейные операции над матрицами.
Рассмотрим матрицы одинаковых размеров:
![]()
![]() ,
, ![]() ,
, ![]() ,….
,….
![]() , если
, если ![]()
![]() , если
, если ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.