Моделирование. Способы обработки экспериментальных данных. Построение моделей колебаний физического маятника

Оглавление

1. МОД. Моделирование. Способы обработки экспериментальных данных  2

2. МОДРегрессионный анализ и моделирование. 8

3. МОД.  Исследование  процессов  с помощью моделей массового обслуживания. 13

4. МОД.  Построение моделей с помощью графов.Численная реализация. 18

5. МОД.  Зачетное занятие. 23

6.  МОД.  Общие возможности имитационного моделирования с помощью инструментального пакета SimuLink  26

7. МОД.  Моделирование процесса массового обслуживания с помощью инструментального пакета Simulink  32

8. МОД.  Построение модели конечного автомата с помощью инструментального пакета Simulink  37

9.  МОД.  Построение моделей колебаний физического маятника. 43

10. МОД.  Зачетное занятие. 48

Моделирование. Способы обработки экспериментальных данных

Код:МОД.

Цель:

Знакомство с основами работы c пакетом MATLAB

Знакомство со статистическими методами обработки результатов экспериментов c помощью пакета MATLAB

Результат обучения:

После успешного завершения занятия пользователь должен:

Знать основные статистические методы обработки экспериментальных данных

Уметь использовать пакет MATLAB для обработки экспериментальных данных

Используемые программы:

MATLAB  2

План занятия:

I.         Работа под руководством преподавателя.                              110 минут

Изучение и использование статистических методов обработки экспериментальных данных с помощью пакета MATLAB.

Самостоятельная работа.                                                                                50 минут

Запуск программы:

Предполагается, что требуемые программы уже инсталлированы на диске.

(См.  «Инструкцию по установке программы на ПК»)

Изучение и использование статистических методов обработки экспериментальных данных с помощью пакета MATLAB.

Рекомендуемое время

110 минут

Знакомство с основами работы в среде MATLAB

Пакет MATLAB является интерактивной системой для выполнения инженерных и научных расчетов, ориентированной на работу с массивами данных. Основным объектом MATLAB является прямоугольный числовой массив – матрица, при этом вектор является частным случаем такого массива, когда число строк (или столбцов) равно 1. С помощью пакета программ MATLAB может выполнять различные операции с векторами и матрицами в режиме непосредственных вычислений без какого либо программирования.

Задание скалярных переменных, векторов и матриц в среде MATLAB.

Запустите программу MATLAB. В появившемся окне в строке приглашения к вводу команд (символ >>). наберите x=1 и нажмите ENTER. После чего на экране появится подтверждение, что скалярная переменная х=1. Чтобы такого подтверждения не было, в конце  директивы надо поставить символ ‘;’ (точка с запятой).

Задание 1.

Задайте самостоятельно следующие значения скалярным переменным:

A=-2;

B=1.14;

C=1.2e-5;

Вектора задаются либо перечислением его элементов (через запятые или пробелы), либо путем задания через двоеточие его начального значения, шага изменения и конечного значения, например:

B=[1 3 5 7];

B=[1:2:7];

B=1:2:7;

Во всех трех случаях вектор B будет содержать элементы {1,3,5,7}

Задание 2.

Введите самостоятельно вектор, состоящий из чисел: 7,4,1,-1.

Введите вектор, состоящий из членов арифметической прогрессии с начальным значением 15, шагом 5 и конечным значением 1000.

Матрицы задаются как последовательность векторов, являющихся ее строками, разделенных символом ‘;’ (точка с запятой) например:

A=[[1 2 3]; [4 5 6]] или

A=[1 2 3; 4 5 6] или

A=[1:1:3; 4:1:6]

Во всех случаях будет введена матрица

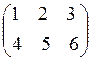А(1,2)=2

A(2,3)=6

Задание 3.

Задание 4.

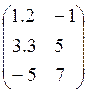Извлеките элемент А(2,2)

1.1.1.  Действия над векторами и матрицами в системе MATLAB

Вектора и матрицы одинаковой размерности можно складывать и вычитать друг из друга, а также делить или умножать на число. Кроме того для векторов и матриц определены векторные и матричные операции умножения. Умножение матриц осуществляется по правилам матричной алгебры, при этом число столбцов в 1- сомножителе должно равняться числу строк во 2-м. Например, пусть заданы вектор а и матрица b:

a=[1,2,3] и b=[0,1,2;2,3,1;2,1,3] тогда

a*b=[10,10,13]

Задание 4.

Введите две матрицы

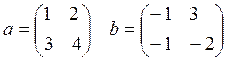c=a + 2*b        и         d=a*b

Результат записать и показать преподавателю.

В системе MATLAB существуют операции поэлементного преобразования векторов и матриц, т.е. операция применяется к каждому элементу матрицы или вектора. К таким операциям принадлежат, например, все элементарные математические функции.

Например, для вектора

x=[1,4,9];         sqrt(x)=[1,2,3]             (sqrt – операция извлечения корня)

Операции поэлементного перемножения и деления векторов и матриц обозначаются как .* и ./ (точка-умножение, точка-деление)

Пример:

a=[1,2,3];        b=[4,5,6];  тогда          a.*b=[4,10,18]

Задание 5.

Пусть дана матрица

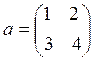Рассчитайте выражение

sqrt(a)./a

Результат записать и показать преподавателю.

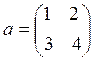Транспонирование матрицы состоит в замене ее строк соответствующими столбцами и наоборот. Таким образом 1- столбец матрицы становится ее 1-й строкой, а 1-я строка  - 1-м столбцом и т.д. Транспонирование вектора приводит к тому, что вектор-строка