




Практическое занятие №3
Тема: Операции над множествами.
Литература: Д.Кук, Г.Бейз Компьютерная математика.М., Наука, 1990г.
В.В.Белов, Е.М.Воробьев, В.Е.Шаталов Теория графов.М., «Высшая школа», 1976г.
Основные сведения из теории.
Множество – это совокупность определенных различаемых объектов, таких, что для любого объекта можно установить, принадлежит этот объект данному множеству или нет.
Список употребляемых понятий и обозначений:
хÎА — элемент х принадлежит множеству А;
хÏA — элемент х не принадлежит множеству А;
AÌ B — А есть подмножество В;
AÍ B — “A B и A¹B” (строгое подмножество);
Æ — пустое множество;
IAI — мощность множества (количество элементов);
AÈB — объединение множеств А и В;
AÇB — пересечение множеств;
A \ B — разность множеств;
A Ù В — “А и В” конъюкция высказываний А и В;
А Ú В — “A или В” дизъюкция высказываний А и В;
AÛB — логическая эквивалентность, А равнозначно В.
Простейшие операции над множествами:
Пусть даны множества А и В. Пересечением множеств А и В называется множество всех элементов, принадлежащих А и В, и обозначается AÇB. Т. е.:
AÇB = {х: хÎА и хÎВ}
Объединение А и В обозначается AÈB и определяется следующим образом:
AÈB = {х: хÎА или хÎВ}
Разность множеств А и В (или дополнение) определяется соотношением A \ B = {х: хÎА и хÏВ} и записывается в виде A \ B.
Пустое множество есть множество, обладающее свойством хÏÆ при любом х.
Второе множество, определение которого зависит от задачи, называют универсальным множеством.
Универсальное множество E есть множество всех рассматриваемых в данной задаче элементов.
Два множества не пересекаются, если AÇB = Æ.
В каждом случае, когда Е задано, определим дополнение множества А (обозначается А') или А' = Е \ А = {х: хÏА}.
Из определений Æ, Е, А следует справедливость тождеств:
АÈА' = Е, AÇА' = Æ.
Диаграмма Ванна.
Пусть Е = {b,c,d,e}, A = {b,c,d}, B = {c,e}. Соответствующая диаграмма изображена на рис. I.
Е
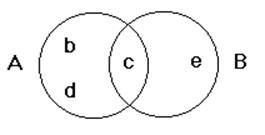
рис.1.
Упражнения для аудиторных занятий.
1. Пусть А – множество целых чисел. Описать словами множество
Х = {х: хÎА и х = 1 или (х-2)ÎХ}
2. Пусть
Е = {1,2,3,4,5}, Х = {1,5},
Y = {1,2,4}, Z = {2,5}.
Найти множества:
а) ХÇY' б) (ХÇZ)ÈY' в) ХÈ(YÇZ) г) (ХÈY)Ç(ХÈZ) д) (ХÈY)' е) Х'ÇY'
ж) (ХÇY)' з) (ХÈY)ÈZ и) ХÈ(YÈZ) к) X\Z л) (X\Z)È(Y\Z).
3. Пусть
Е = {a,b,c,d,e,f}, A = {a,b,c},
B = {f,e,c,a}, C = {d,e,f}.
Найти множества:
а) А\С б) В\С в) С\В
г) А\В д) А'ÈВ е) ВÇА'
ж) АÇС з) СÇА и)СÙА
4. Даны два произвольных множества А и В такие, что АÇВ = Æ. Что представляют собой множества А\В и В\А?
5. Дано произвольное множество Х. Найти множества:
а) ХÇХ' б) ХÈХ' в) Х\Х'.
6. Какие из следующих условий справедливы?
а) 0ÎÆ б) Æ = {0} в) ½{Æ}½ = 1
7. найти следующие множества:
а) {1,2}+{1,3} б) {1,2}\ {1,3} в) {1,2}È{1,3} г) {1,2}\ {1,3}
д) {1,2}*{1,3} е) {1,2}-{1,3} ж) {2,4}/ {2} з) {2,4}-{2}
8. Как можно представить следующие множества, используя диаграммы Венна:
{A, {A}}, {{a}, {б}}, {X,Y,Z}, где
X = {x: х = 1 или (х-2)ÎХ},
Y = {x: x = 3 или (х-3)ÎY},
Z = {x: х = 2 или (х-2)ÎZ}.
9. Доказать, что АÇ(ВÇС) = (АÇВ)ÇС.
10. Пусть Х = {a,b,c} и Y = {a,b,c,f}. Найти Х *Y и Y2.
Упражнения для домашних занятий.
1. Какие из приведенных определений являются правильными?
А = {1,2,3},
В = {5,6,66,7},
С = { х: хÏА},
Д = {А,С},
Е = { x: х = 1 или х = {y} и уÎЕ}.
2. Описать словами следущие множества:
(YÇ(KÈL))'È(H\L),
(PÈRÈQ)\(PÇ(Q\R)),
((E\F)È(F\E))'ÈG.
3. Доказать эквивалентность следующих утверждений, т. е. что из каждого следует другое:
а) АÈВ = Е б) А'ÍВ в) А'ÇВ' = Æ.
Практическое занятие №4
Тема: Алгоритмы размещения.
I. Последовательно-итерационный алгоритм размещения вершин графа на плоскости с минимизацией СДС (суммарная длина соединений).
Задан граф G(X,U), отображающий схему и коммутационное монтажное пространство, на котором размещен Gr(дискретная сетка посадочных мест элементов на типовой плате). Необходимо разместить все вершины xiÎX в узлы сетки с минимизацией суммарной длины ребер uiÎU. Часть элементов размещена вручную (если нет, то первый элемент закрепляется произвольно). Разместим вершину xi в (j+1) позицию, где j – число занятых позиций. Введем понятие коэффициента связанности Δ(xi) = ai,h-ai,z, где ai,h – число ребер, соединяющих вершину xi с подмножеством ранее размещенных вершин графа, ai,z = ρ(xi)- ai,h – число ребер, соединяющих вершину xi с неразмещенными вершинами графа. Тогда Δ(xi) = 2ai,h- ρ(xi), где ρ(xi) – степень вершины xi.
Идея алгоритма заключается в определении коэффициента связности для всех неразмещенных вершин и в помещении в первую свободную позицию рядом с размещенной вершиной вершины с максимальным значением Δ(xi). Последовательно рассматривая все вершины графа, выполняют их размещение.
Алгоритм можно использовать при размещенииразногабаритных элементов, но с кратными размерами. В этом случае КП покрывается масштабной сеткой, линейные размеры дискретов которой равны минимальным размерам элементов. При размещении элемента, кратного нескольким дискретам, в список занятых позиций заносят все те элементарные позиции, которые он занимает.
Итерационная часть алгоритма заключается в парной перестановке некоторых вершин графа G(X,U) и в оценке СДС при каждой замене. Замена целесообразна, если СДС при этом уменьшается. Среди всех вершин графа выбираются претенденты для замены. Для этого просматривается матрица расстояний Д, отображающая расстояния между элементами как результат размещения вершин графа схемы G(X,U) на дискретном поле последовательным алгоритмом. Множество инцедентных ребер Ui для каждой вершины xiÎX разбивается на два непересекающихся подмножества Ui' и Ui''. К подмножеству Ui' (α - ребра) относятся «короткие» ребра, вес которых не превышает некоторого значения α, равного 2—3. вес ребра отражает расстояние между связываемыми им вершинами. К подмножеству Ui'' (β - ребра) относятся остальные ребра («длинные» ребра). Для каждой вершины подсчитывается разность Δi = ½Ui''½-½ Ui'½.
Поиск вершин, которые являются претендентами на замену, осуществляется среди тех вершин, для которых Δi>0. Первым претендентом (вершина xi) является вершина, имеющая наибольшее положительное значение Δi.
Для поиска второй вершины (вершина хJ) – претендента на замену
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.