Пользовательский элемент управления. Создание клиентского приложения. Развитие серверного проекта, страница 9

Другой очень важной характеристикой систем автоматического регулирования является импульсная переходная функция ИПФ. Она представляет собой решение приведенного выше уравнения при входном воздействии, которое имеет вид идеального импульса, или функции Дирака u(t) = d(t).

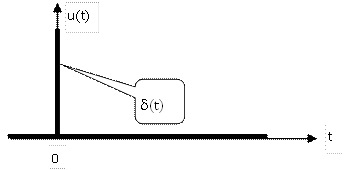
Эта функция является особой. Ее свойства изучаются в теории обобщенных функций, так как для классического матанализа она слишком сложна. Дело в том, что амплитуда скачка d(t) в момент времени t = 0 стремится к бесконечности, в то время как площадь под кривой остается равной единице. На практике входное воздействие такого типа не реализуемо, но оно удобно для анализа систем управления, так как является идеализацией короткого импульсного воздействия. Функция Дирака d(t) очень часто используется для оценки поведения систем во время подачи на их вход коротких импульсных сигналов. Качество процесса, возбуждаемого сигналом такого рода, считается важной характеристикой системы.

Наш элемент управления PlotControl по умолчанию (в качестве товарного знака) изображает именно такую ИПФ (осциллирующего типа). Такое поведение заложено в его структуру на этапе разработки. Убедитесь, что в конструкторе класса Graph стоит вызов метода SetDefaultPlot, который при вычислении ординат графика вызывает функцию OscillatingDelta с параметрами соответствующими постоянной времени 0.08, декременту затухания 0.12 и коэффициенту усиления 10. Смотри оператор:

points[i].Y = (float)OscillatingDelta (points[i].X, 0.08, 0.12, 10);

Вспомним, что общее решение однородного дифференциального уравнения не зависит от типа воздействия. От него зависит лишь частное решение неоднородного дифференциального уравнения. С учетом установившегося режима (y(t) ®0 при t®¥), получим .

Для того, чтобы понять алгоритм функции OscillatingDelta (выражение, которое вычисляет реакцию системы), надо получить переходную составляющую решения . Если искать постоянные интегрирования из начальных условий (которые вроде бы остались теми же), то мы получим абсурд A=B=0.

Здесь становится понятной суть использования теории обобщенных функций. Классический матанализ, как видите, дает отказ, так как он говорит, что производная от функции Дирака в момент t = 0 не существует. В теории же обобщенных функций функция Дирака является производной от функции Хевисайда.

Ее можно также рассматривать как предел разности двух ступенчатых функций.

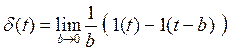
Вторая сдвинута во времени на промежуток b. Такой подход удовлетворяет условию, при котором площадь под кривой все время остается  равной единице.

Используя этот результат, будем искать новое решение (ИПФ) в виде производной от старого решения (ПФ). Напомним, что оно было получено при воздействии типа 1(t). В частном случае комплексных корней (см. формулу ***) получим.

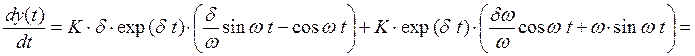
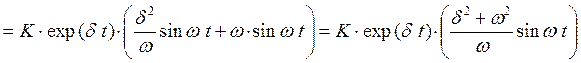
В терминах декремента затухания и колебательности получим другое (эквивалентное) выражение.

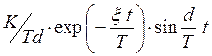
Именно это выражение запрограммировано в функции OscillatingDelta.

Задание

При развитии клиентского приложения поставим следующую задачу. Ввести возможность выбора пользователем одной из нескольких доступных функций, а также добавить элементы управления, которые позволят исследовать влияние параметров системы управления (декремент затухания, колебательность, постоянные времени) на качество переходных процессов. Видимость (доступность или смысл текстовых меток) элементов управления, очевидно, должна зависеть от типа выбранной функции.

Для того, чтобы вы могли сконцентрироваться на интерфейсной части приложения, приведем возможные варианты реализации самих функций. Заметьте, что функция OscillatingDelta должна быть вновь реализована в клиентском приложении, так как ее реализация в сервере — это всего лишь "товарный знак", случайно совпавший с целью исследований, которые мы проводим в рамках клиентского приложения.

//==== Колебательный переходный процесс

double Oscillating (double x,  double T, double c, double k)