Напомним, что общее решение уравнения (*) при произвольном
виде входного воздействия состоит из двух составляющих: ![]() .
Первая составляющая — это переходная функция, оня является фундаментальным
решением однородного уравнения (того же уравнения, но при u(t) = 0) и характеризует
свойства самой системы. Вторая составляющая представляет собой одно из решений
неоднородного уравнения (*).
Оно зависит как от свойств системы, так и от входного сигнала. Выбор решения
произволен. Например, в качестве
.
Первая составляющая — это переходная функция, оня является фундаментальным
решением однородного уравнения (того же уравнения, но при u(t) = 0) и характеризует
свойства самой системы. Вторая составляющая представляет собой одно из решений
неоднородного уравнения (*).
Оно зависит как от свойств системы, так и от входного сигнала. Выбор решения
произволен. Например, в качестве ![]() можно взять выход
системы в установившемся режиме (при t®¥).
Обычно так и делают, так как найти это решение очень просто. В нашем случае им
является:
можно взять выход
системы в установившемся режиме (при t®¥).
Обычно так и делают, так как найти это решение очень просто. В нашем случае им
является:
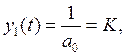 K — имеет смысл коэффициента усиления
системы
K — имеет смысл коэффициента усиления
системы
Простой подстановкой этого решения в уравнение (*) вы можете
убедиться, что оно ему удовлетворяет. Переходную ![]() составляющую
общего решения определяют с помощью характеристического
уравнения. Так называется алгебраическое уравнение вида:
составляющую
общего решения определяют с помощью характеристического
уравнения. Так называется алгебраическое уравнение вида:
![]() , полученное на основе исходного — дифференциального. Корни
уравнения
, полученное на основе исходного — дифференциального. Корни
уравнения ![]() определяют поведение системы в переходном
режиме. Говорят, что они характеризуют свободное движение системы. Заметим, что
эти же корни являются собственными числами матрицы системы дифференциальных
уравнений первого порядка при эквивалентном описании задачи в пространстве
состояний. В нашем случае уравнение (*) второго порядка эквивалентно системе
из двух уравнений первого порядка. Переходная составляющая (свободное движение,
или общее решение однородного уравнения) имеет вид.
определяют поведение системы в переходном
режиме. Говорят, что они характеризуют свободное движение системы. Заметим, что
эти же корни являются собственными числами матрицы системы дифференциальных
уравнений первого порядка при эквивалентном описании задачи в пространстве
состояний. В нашем случае уравнение (*) второго порядка эквивалентно системе
из двух уравнений первого порядка. Переходная составляющая (свободное движение,
или общее решение однородного уравнения) имеет вид.
![]()
Здесь A и B — постоянные интегрирования, определяемые из начальных условий. Именно они обеспечивают единственность общего решения. Итак, общее решение неоднородного уравнения (*) при единичном ступенчатом воздействии имеет вид.
![]()
Обратите внимание на то, что в установившемся режиме (когда затухнут экспоненты) выходной сигнал будет равен K, то есть единица на входе усилится в K раз. Нам осталось найти коэффициенты A и B, с учетом начальных условий. В качестве начальных обычно принимают условия равенства нулю как самого сигнала y(0) = 0, так и его первой производной. Таким образом, постоянные интегрирования можно найти, решив систему из двух алгебраических уравнений:
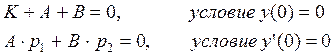
Решив эту систему, найдем выражения для постоянных интегрирования.
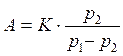
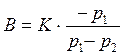
Подстановка найденных констант в общее решение дает.
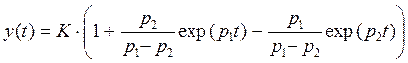 (**)
(**)
Корни характеристического
уравнения ![]() могут быть действительными, кратными и
комплексными, В связи с этим различают:
могут быть действительными, кратными и
комплексными, В связи с этим различают:
¨ Апериодические процессы, соответствующие отрицательным действительным корням уравнения,
¨ Осциллирующие процессы, соответствующие паре сопряженных комплексных корней с отрицательной действительной частью.
¨ Отдельно
рассматривают случай кратных корней ![]() . При этом решение
является полиномом от t.
. При этом решение
является полиномом от t.
![]()
¨
Также отдельно рассматривают случаи положительных действительных
корней или комплексных корней с положительной действительной частью. Им
соответствуют неустойчивые системы, так как в этих случаях с течением времени
функция ![]() неограниченно растет.
неограниченно растет.
Осциллирующее решение можно получить из выражения (**) путем подстановки в него пары сопряженных комплексных корней:
![]()
Здесь ![]() — действительная и
мнимая части корней. Они зависят из коэффициентов
— действительная и
мнимая части корней. Они зависят из коэффициентов ![]() исходного
уравнения.
исходного
уравнения.
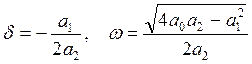
Для упрощения выражения, которое получится в результате подстановки комплексных корней в решение (**), удобно использовать формулы Эйлера:
![]()
![]()
Получим:
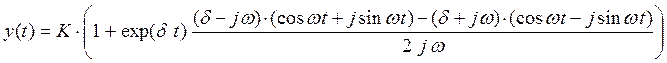
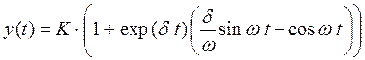 (***)
(***)
Последнее решение часто записывают в эквивалентном виде с помощью параметров, имеющих определенный физический смысл. Введем новые понятия.
Декремент затухания: 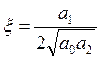 ,
постоянная времени:
,
постоянная времени: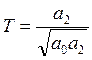 колебательность:
колебательность: ![]()
Выражения для ![]() (действительной и
мнимой частей корней) перепишем в виде:
(действительной и
мнимой частей корней) перепишем в виде:
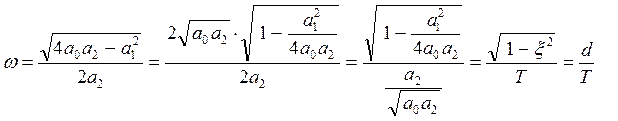
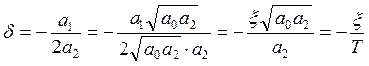
Подставив эти выражения в осцилирующее решение (***), получим эквивалентную запись.
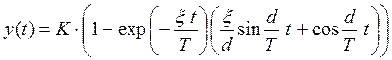 (****)
(****)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.