Экспериментальное определение теплоемкости металлов при комнатной температуре и сравнение с теоретическими данными, страница 2

Максимальная частота фононов соответствует колебаниям с длиной волны порядка межатомного расстояния и носит название Дебаевской частоты ω_D. Она равна , где а – постоянная кристаллической решетки. Дебаевской частоте можно поставить в соответствие характеристическую температуру – температуру Дебая Θ:   ћω_D = kΘ и  отсюда  Θ = ћω_D/k, где k – постоянная Больцмана.

Конечно, фонон это не частица в буквальном смысле слова, а квазичастица. Просто величины, описывающие макроскопические свойства твердых тел, выражаются в терминах, характеризующих отдельные квазичастицы: их скорость, длину свободного пробега и т.д. Для квазичастиц могут не выполняться некоторые обычные соотношения, например, для фононов понятие массы теряет смысл, т.к. отношение между энергией и импульсом не равно E=p²/(2m), а зависит от величины импульса, т.е. масса изменяется (причиной этого является периодическая структура кристалла). П. Дебай предложил считать, что для фононов линейный закон дисперсии справедлив для всего диапазона частот и волновых векторов.

В твердом теле колебания среды, т.е. звуковые волны, могут быть продольными и поперечными, причем имеются две независимые поперечные поляризации. Поэтому у фонона одной и той же энергии (импульсу) могут соответствовать три различных состояния. Это означает, что состояния с этой энергией трехкратно вырождены. С другой стороны, известно, что степень вырождения равна 2J+1, где J – спин частицы. Поэтому формально фонону можно приписать спин 1, а это означает, что фонон является бозе-частицей.

Энергия квантового гармонического осциллятора может иметь значения:

ε_n = (n+1)ћω (n=0,1,2,…)

Средняя энергия одного осциллятора с учетом того, что фононы подчиняются статистике Бозе-Эйнштейна, равна

Умножив на число осцилляторов в единице объема, получим при заданной температуре Т энергию единицы объема кристалла U:

.

Здесь U₀ – энергия нулевых колебаний кристалла. В общем случае продольные и поперечные волны имеют разную скорость, поэтому здесь v_зв является средней скоростью звуковых волн в кристалле.

В случае низких температур T<<Θ возбуждаются лишь фононы с низкой энергией, т.е. длинноволновые фононы и энергия U_ф равна

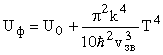
Отсюда решеточная теплоемкость при низких температурах равна

.

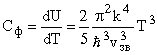Таким образом, при низких температурах C_ф ~ T³. Это и есть закон Т³ Дебая для теплоемкости твердых тел при низких температурах.

В случае высоких температур T>Θ возбуждаются в основном фононы максимально возможной частоты, что связано с зависимостью плотности фононных состояний от волнового вектора - она пропорциональна k². Энергия кристалла равна средней энергии фонона ћω_D, умноженной на их число <n> и на 3N число мод (видов колебаний) в единице объема:

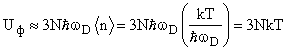
Соответственно теплоемкость при высоких температурах равна C_ф=3Nk. Для одного моля вещества N=N_A и C_ф=3R≈25 Дж/(моль К), где R – газовая постоянная. Это есть закон Дюлонга и Пти, гласящий, что теплоемкость любого твердого тела не зависит от температуры и определяется только числом его атомов в единице объема.

 

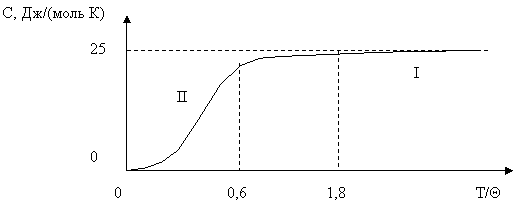Рис. 1. Зависимость теплоемкости твердого тела от температуры.