Экзаменационные билеты № 1-25 по курсу "Теория алгоритмических языков и компиляторов" (Предварительные математические сведения. Метаязык. Основные способы определения терминальных и нетерминальных символов)

МОСКОВСКИЙ ИНСТИТУТ ЭЛЕКТРОННОЙ ТЕХНИКИ

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ N  1

по курсу Теория алгоритмических языков и компиляторов МП-35,30,38

1. Предварительные математические сведения. Основные понятия теории множеств. Операции над множествами. Свойства множеств.

2. Задача

Дана грамматика G с набором правил

S -> for ( ; A; ;) | I = D

A -> I < D

I -> B | IB

B -> r | o | f

D -> C | CD

C -> 0|1|2|3|4|5|6|7|8|9

a) Преобразовать грамматику и построить  детерминированный  магазинный автомат.

б) Привести пример разбора предложения языка L(G).

Билет рассмотрен и утвержден на заседании кафедры "___"_________2002г.

МОСКОВСКИЙ ИНСТИТУТ ЭЛЕКТРОННОЙ ТЕХНИКИ

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ N  2

по курсу Теория алгоритмических языков и компиляторов МП-30,35,38

1. Произведение множеств. Отношения. Графы и деревья. Строки, формальные языки, операции над языками.

2. Задача

Дана грамматика G с набором правил

S -> for ( ; A; ;) | I = D

A -> I < D

I -> B | IB

B -> r | o | f

D -> C | CD

C -> 0|1|2|3|4|5|6|7|8|9

a) Если данная грамматика LL(1)- грамматика , тогда необходимо  построить  детерминированный  магазинный автомат. Если грамматика не LL(1) - грамматика, тогда необходимо построить недетерминированный магазинный автомат, моделирующий левосторонний вывод.

б) Привести пример разбора предложения языка L(G).

Билет рассмотрен и утвержден на заседании кафедры "___"_________2002г.

Заведующий кафедрой ____________________

МОСКОВСКИЙ ИНСТИТУТ ЭЛЕКТРОННОЙ ТЕХНИКИ

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ N  3

по курсу Теория алгоритмических языков и компиляторов МП-30,35,38

1. Способы определения языковых процессоров. Формальные грамматики. Классификация грамматик.

2. Задача

Дана грамматика G с набором правил

S -> for ( ; A; ;) | I = D

A -> I < D

I -> B | IB

B -> r | o | f

D -> C | CD

C -> 0|1|2|3|4|5|6|7|8|9

a) Если данная грамматика LL(1)- грамматика , тогда необходимо  построить  детерминированный  магазинный автомат. Если грамматика не LL(1) - грамматика, тогда необходимо построить недетерминированный магазинный автомат, моделирующий правосторонний вывод.

Билет рассмотрен и утвержден на заседании кафедры "___"_________2002г.

Заведующий кафедрой ____________________

---------------------------------------------------------------------

МОСКОВСКИЙ ИНСТИТУТ ЭЛЕКТРОННОЙ ТЕХНИКИ

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ N  4

по курсу Теория алгоритмических языков и компиляторов МП-30,35,38

1.  Основные типы контекстно-свободных грамматик. s-грамматики, q-грамматики.

2. Задача

Дана грамматика G с набором правил

S -> while (A) I = D | I = D

A -> I < D

I -> B | IB

B -> f | w | h | i | l | e | k

D -> C | CD

C -> 0|1|2|3|4|5|6|7|8|9

a) Преобразовать грамматику и построить  детерминированный  магазинный автомат.

б) Привести пример разбора предложения языка L(G).

Билет рассмотрен и утвержден на заседании кафедры "___"_________2002г.

Заведующий кафедрой ____________________

МОСКОВСКИЙ ИНСТИТУТ ЭЛЕКТРОННОЙ ТЕХНИКИ

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ N  5

по курсу Теория алгоритмических языков и компиляторов МП-30,35,38

1. Основные типы контекстно-свободных грамматик. LL и LR -грамматики.

2. Задача

Дана грамматика G с набором правил

S -> while (A) I = D | I = D

A -> I < D

I -> B | IB

B -> f | w | h | i | l | e | k

D -> C | CD

C -> 0|1|2|3|4|5|6|7|8|9

a) Если данная грамматика LL(1)- грамматика , тогда необходимо  построить  детерминированный  магазинный автомат. Если грамматика не LL(1) - грамматика, тогда необходимо построить недетерминированный магазинный автомат, моделирующий левосторонний вывод.

б) Привести пример разбора предложения языка L(G).

Билет рассмотрен и утвержден на заседании кафедры "___"_________2002г.

Заведующий кафедрой ____________________

МОСКОВСКИЙ ИНСТИТУТ ЭЛЕКТРОННОЙ ТЕХНИКИ

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ N  6

по курсу Теория алгоритмических языков и компиляторов МП-30,35,38

1. Распознаватели. Язык, определяемый распознавателем. Разбор строк. Восходящий и нисходящий анализ.

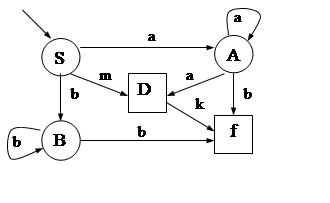
2. Дан автомат А, заданный графом состояний, отдельным для каждого варианта.

Необходимо:

·  Найти грамматику G, такую, чтобы язык допускаемый автоматом T(A) был эквивалентен языку, порождаемому грамматикой L(G), т.е. L(G)=T(A).

·  Определить язык Т(А).

·  Ответить на вопрос «Является ли граф состояний детерминированным?». Если не является, надо построить детерминированный автомат и показать формальный вывод функций перехода для детерминированного автомата.

·  Привести пример разбора предложения языка L(G).

  

\Билет рассмотрен и утвержден на заседании кафедры "___"_________2002г.

Заведующий кафедрой ____________________

МОСКОВСКИЙ ИНСТИТУТ ЭЛЕКТРОННОЙ ТЕХНИКИ

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ N  7

по курсу Теория алгоритмических языков и компиляторов МП-30,35,38

1. Детерминированные и недетерминированные конечные автоматы. Моделирование конечного автомата.

2. Задача

Дана грамматика G с набором правил

S -> while (A) I = D | I = D

A -> I < D

I -> B | IB

B -> f | w | h | i | l | e | k

D -> C | CD

C -> 0|1|2|3|4|5|6|7|8|9

a) Если данная грамматика LL(1)- грамматика , тогда необходимо  построить  детерминированный  магазинный автомат. Если грамматика не LL(1) - грамматика, тогда необходимо построить недетерминированный магазинный автомат, моделирующий правосторонний вывод.

б) Привести пример разбора предложения языка L(G).

Билет рассмотрен и утвержден на заседании кафедры "___"_________2002г.

Заведующий кафедрой ____________________

МОСКОВСКИЙ ИНСТИТУТ ЭЛЕКТРОННОЙ ТЕХНИКИ

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ N  8

по курсу Теория алгоритмических языков и компиляторов МП-30,35,38

1. Недетерминированные автоматы с магазинной памятью.  Конфигурация магазинного автомата. Граф состояний.

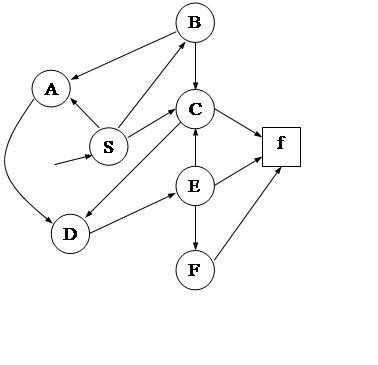
2. Задача. Дан автомат А, заданный графом состояний, отдельным для каждого варианта.

Необходимо:

·  Найти грамматику G, такую, чтобы язык допускаемый автоматом T(A) был эквивалентен языку, порождаемому грамматикой L(G), т.е. L(G)=T(A).

·  Определить язык Т(А).

·  Ответить на вопрос «Является ли граф состояний детерминированным?». Если не является, надо построить детерминированный автомат и показать формальный вывод функций перехода для детерминированного автомата.

·  Привести пример разбора предложения языка L(G).

 

b                         b

a                       

d                 k                     d

k                                             a            

a

k                                

c                                a

c

Билет рассмотрен и утвержден на заседании кафедры "___"_________2002г.

Заведующий кафедрой ____________________

МОСКОВСКИЙ ИНСТИТУТ ЭЛЕКТРОННОЙ ТЕХНИКИ

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ N  9

по курсу Теория алгоритмических языков и компиляторов