






|
№ |
Вопросы |
Варианты ответов |
|
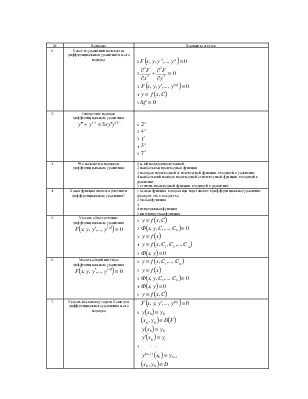
1. |
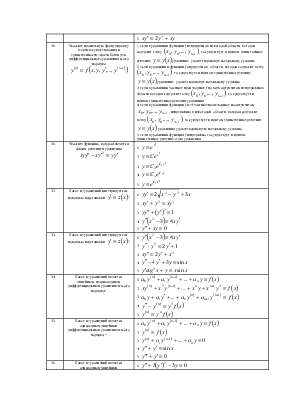
Какое из уравнений называется дифференциальным уравнением n-ого порядка. |
1. 2. 3. 4. 5. |
|
2. |
Определите порядок дифференциального уравнения |
1. 2. 3. 4. 5. |
|
3. |
Что называется порядком дифференциального уравнения |
1. n-ый порядок производной 2. наибольшая производная функции 3. порядок производной от неизвестной функции, входящей в уравнение 4. наибольший порядок производной от неизвестной функции, входящей в уравнение 5. степень производной функции, входящей в уравнение |
|
4. |
Какая функция является решением дифференциального уравнения? |
1. всякая функция, которая при подстановке в дифференциальное уравнение обращает его в тождество 2. любая функция 3. 4. непрерывная функция 5. интегрируемая функция |
|
5. |
Указать общее решение дифференциального уравнения |
1. 2. 3. 4. 5. |
|
6. |
Указать общий интеграл дифференциального уравнения |
1. 2. 3. 4. 5. |
|
7. |
Указать постановку задачи Коши для дифференциального уравнения n-ого порядка |
1. 2. 3. 4. 5. |
|
8. |
Какая из заданных функций является общим решением
уравнения |
1. 2. 3. 4. 5. |
|
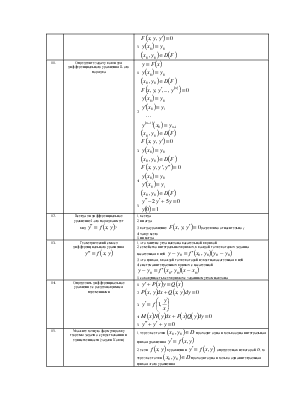
9. |
Какая из функций является решением задачи Коши |
1. 2. 3. 4. 5. |
|
10. |
Определите задачу Коши для дифференциального уравнения I-ого порядка |
1. 2. 3. 4. 5. |
|
11. |
Определите задачу коши для дифференциального уравнения II-ого порядка |
1. 2. 3. 4. 5. |
|
12. |
Всегда ли дифференциальное уравнение I-ого
порядка имеет вид |
1. всегда 2. иногда 3. когда уравнение 4. чаще всего 5. никогда |
|
13. |
Геометрический смысл дифференциального уравнения |
1. это тангенс угла наклона касательной к кривой 2. семейство интегральных
кривых, в каждой точке которых заданна касательная к ней 3. это кривая, в каждой точке которой известна касательная к ней 4. система интегральных
кривых с касательной 5. совокупность всех кривых с заданным углом наклона |
|
14. |
Определить дифференциальное уравнение с разделяющимися переменными |
1. 2. 3. 4. 5. |
|
15. |
Укажите точную формулировку теоремы задачи о существовании и единственности (задачи Коши) |
1. через все точки 2. если 3. пусть функция 4. решение задачи Коши заполняет всю область D 5. пусть функция |
|
16. |
Какое из уравнений является дифференциальным уравнением с разделяющимися переменными? |
1. 2. 3. 4. 5. |
|
17. |
Какая из функция является однородной? |
1. 2. 3. 4. 5. |
|
18. |
Каков порядок однородной функции |
1. 2. 3. не является однородной 4. 5. |
|
19. |
Какое из уравнений I-ого порядка является однородным? |
1. 2. 3. 4. 5. |
|
20. |
Какое из уравнений I-ого порядка
интегрируется с помощью замены |
1. линейное 2. уравнение Бернулли 3. однородное 4. с разделяющимися переменными 5. ни одного из известных дифференциальных уравнений I-ого порядка |
|
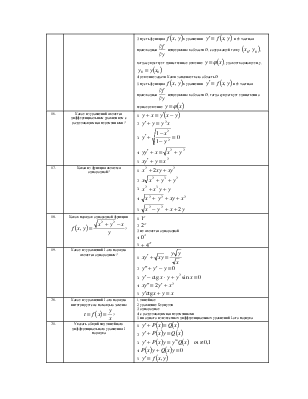
21. |
Указать общий вид линейного дифференциального уравнения I порядка |
1. 2. 3. 4. 5. |
|
22. |
Какое из уравнений является линейным I-ого порядка? |
1. 2. 3. 4. 5. |
|
23. |
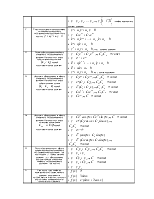
Решением какого уравнения является следующая формула:
|
1. однородное 2. уравнение Бернулли 3. с разделяющимися переменными 4. линейного I-ого порядка 5. линейного II-ого порядка |
|
24. |
Каким методом ищется решение линейного дифференциального уравнения I-ого порядка? |
1. подстановкой 2. методом Бернулли 3. заменой 4. заменой 5. заменой |
|
25. |
Какое уравнение интегрируется с помощью подстановки |
1. 2. 3. 4. 5. |
|
26. |
Какое из уравнений называется уравнением Бернулли? |
1. 2. 3. 4. 5. |
|
27. |
Какое из уравнений интегрируется с помощью
подстановки |
1. 2. 3. 4. 5. |
|
28. |
Определить тип дифференциального уравнения |
1. с разделяющимися переменными 2. линейное I-ого порядка 3. уравнение Бернулли 4. однородное 5. линейное II-ого порядка |
|
29. |
Какое из уравнений является уравнением Бернулли? |
1. 2. 3. 4. 5. |
|
30. |
Укажите правильную формулировку теоремы существования
и единственности задачи Коши для дифференциального уравнения n-ого
порядка |
1. если в уравнении функции f
непрерывна в некоторой области, которая содержит точку 2. если в уравнении функции f
определена в области, которая содержит точку 3. если в уравнении частные
производные f по всем аргументам непрерывны в области которая
содержит точку 4. если в уравнении функции f
и её частные производные по аргументам 5. если в уравнении функция f непрерывна то существует и притом единственное решение этого уравнения |
|
31. |
Укажите функцию, которая является общим решением
уравнения |
1. 2. 3. 4. 5. |
|
32. |
Какое из уравнений интегрируется с помощью
подстановки |
1. 2. 3. 4. 5. |
|
33. |
Какое из уравнений интегрируется с помощью
подстановки |
1. 2. 3. 4. 5. |
|
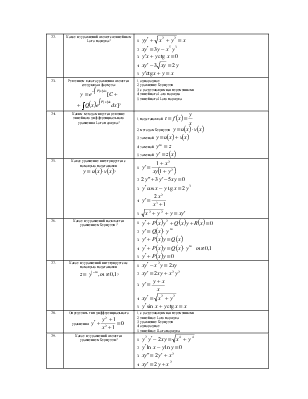
34. |
Какое из уравнений является линейным, неоднородным дифференциальным уравнением n-ого порядка? |
1. 2. 3. 4. 5. |
|
35. |
Какое из уравнений является однородным линейным дифференциальным уравнением n-ого порядка ? |
1. 2. 3. 4. 5. |
|
36. |
Какое из уравнений является однородным линейным дифференциальным уравнением n-ого порядка? |
1. 2. 3. 4. 5. |
|
37. |
Если y1 и y2 – частные линейно независимые решения уравнения |
1. 2. 3. 4. 5. |
|
38. |
Если y1 и y2 – частные линейно независимые решения уравнения |
1. 2. 3. 4. 5. |
|
39. |
Указать определитель Вронского дифференциальных функций y1 и y2 |
1. 2. 3. 4. 5. |
|
40. |
Определить линейно-независимые функции |
1. 2. 3. 4. 5. |
|
41. |
Если вронскиан |
1. линейно независимы 2. 3. 4. 5. линейно зависимы |
|
42. |
Указать формулу Лиувилля |
1. 2. 3. 4. 5. |
|
43. |
Если известно одно частное решение y1 уравнения |
1. 2. 3. 4. 5. |
|
44. |
Пусть |
1. 2. 3. 4. 5. |
|
45. |
Определить характеристическое уравнение для
дифференциального уравнения n-ого порядка |
1. 2. 3. 4. 5. |
|
46. |
Какое частное решение соответствует действительному корню с кратностью единицы характеристического уравнения для однородного линейного дифференциального уравнения n-ого порядка? |
1. 2. 3. 4. 5. |
|
47. |
Какое частное решение соответствует действительному корню с кратностью r характеристического уравнения для однородного линейного дифференциального уравнения II-ого порядка? |
1.
r линейно независимых частных решений 2. 2. линейно независимые
решения 3. 4. 5. |
|
48. |
Какое частное решение соответствует паре комплексно
сопряжённых корней |
1. 2. 3. 4. 5. |
|
49. |
Какое решение соответствует каждой паре комплексно
сопряжённых корней |
1. 2. 3. 4. 5. |
|
50. |
Указать характеристическое уравнение для линейного однородного дифференциального уравнения II-ого порядка |
1. 2. 3. 4. 5. |
|
51. |
Указать характеристическое уравнение для линейного
однородного дифференциального уравнения II-ого порядка |
1. 2. 3. 4. 5. |
|
52. |
Укажите общее решение линейного однородного
дифференциального уравнения II-ого порядка в случае действительных и различных |
1. 2. 3. 4. 5. |
|
53. |
Определить общее решение линейного однородного
дифференциального уравнения II-ого порядка в случае действительных и равных |
1. 2. 3. 4. 5. |
|
54. |
Определить общее решение линейного однородного
дифференциального уравнения II-ого порядка в случае комплексно сопряжённых |
1. 2. 3. 4. 5. |
|
55. |
Указать формулировку для общего решения неоднородного линейного дифференциального уравнения n-ого порядка, если yr – частное решение уравнения , а y0 – общее решение соответствующего однородного линейного дифференциального уравнения n-ого порядка |
1. 2. 3. 4. 5. |
|
56. |
Если правая часть линейного неоднородного дифференциального уравнения с постоянными коэффициентами имеет вид, то в каком случае частное решение находится только методом Лагранжа? |
1. 2. 3. 4. 5. |
|
57. |
При каком виде правой части неоднородного дифференциального уравнения с постоянными коэффициентами частное решение можно строить методом подбора? |
1. 2. 3. 4. 5. |
|
58. |
Определить общее решение уравнения |
1. 2. 3. 4. 5. |
|
59. |
Какое из уравнений является линейным неоднородным дифференциальным уравнением II-ого порядка? |
1. 2. 3. 4. 5. |
|
60. |
Определить функцию, являющуюся частным решением
уравнения |
1. 2. 3. 4. 5. |
|
61. |
Какое уравнение интегрируется только методом вариации произвольных постоянных? |
1. 2. 3. 4. 5. |
|
62. |
Какое из уравнений является линейным неоднородным дифференциальным уравнением II-ого порядка с постоянными коэффициентами? |
1. 2. 3. 4. 5. |
|
63. |
Указать общее решение уравнения |
1. 2. 3. 4. 5. |
|
64. |
Какое из уравнений может интегрироваться методом подбора частного решения? |
1. 2. 3. 4. 5. |
|
65. |
Какие две данные функции линейно зависимы? |
1. 2. 3. 4. 5. |
|
66. |
Какое из уравнений является линейным однородным III-его порядка? |
1. 2. 3. 4. 5. |
|
67. |
Дано общее решение однородного уравнения |
1. 2. 3. 4. 5. |
|
68. |
Какой вид должны иметь правая часть неоднородного линейного дифференциального уравнения с постоянными коэффициентами, чтобы его частное решение строилось методом подбора? |
1. 2. 3. 4. 5. |
|
69. |
В каком виде ищется частное решение неоднородного линейного дифференциального уравнения с постоянными коэффициентами со специальной правой частью? |
1. 2. 3. 4. 5. |
|
70. |
Чему равно r в формуле |
1. 2. 3. 4. 5. |
|
71. |
Чему равно r в формуле |
1. 2. 3. 4. 5. |
|
72. |
Чему равно r в формуле |
1. 2. 3. 4. 5. |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.