


























Поняття похідної функції та її геометричний, фізичний і економічний зміст. Зв'язок між диференційованістю і неперервністю функції. Таблиця похідних. Похідна суми, різниці, частки і добутку функцій. Похідна складеної функції. Похідна неявної функції. Диференціал функції. Похідні та диференціали вищих порядків. Формула Тейлора. Правило Лопіталя.
Тема 1.18. Частинні похідні і повний диференціал функції кількох змінних
Частинний і повний прирости функції двох змінних та їх економічне тлумачення. Частинні похідні функції двох змінних та їх геометричне тлумачення. Частинні еластичності. Повний диференціал функції двох змінних, його геометричний зміст та застосування до наближених обчислень. Похідна за напрямом та градієнт функції двох змінних. Частинні похідні та диференціали вищих порядків функції двох змінних.
Розділ 8. ГРАНИЧНИЙ (МАРГІНАЛЬНИЙ) АНАЛІЗ
Тема 1.19. Застосування диференціального числення функції однієї змінної в економічному аналізі.
Граничні витрати, дохід і прибуток. Максимізація прибутку і маргінальний аналіз. Аналіз витрат: визначення ліквідаційної ціни продукції фірми і найменші маргінальні витрати на ресурси. Аналіз маргінальної продуктивності. Еластичність попиту і пропозицій, виробничих функцій і т.п..
Тема 1.20. Застосування диференціального числення функції кількох змінних в економічному аналізі
Виробничі функції кількох змінних і граничний аналіз. Частинні граничні витрати, дохід і прибуток. Максимізація прибутку і мінімізація витрат. Частинні еластичності функції та їх економічна інтерпретація.
Розділ 9. ДОСЛІДЖЕННЯ ФУНКЦІЙ ТА ПОБУДОВА ЇХ ГРАФІКІВ
Тема 1.21. Застосування похідної функції до дослідження функцій та побудови їх графіків
Умови зростання і спадання функції. Локальний екстремум функції та його знаходження. Найбільше і найменше значення функції на проміжку. Опуклість і вгнутість графіка функції. Точки перегину. Асимптоти графіка функції. Схема дослідження функції та побудови її графіка.
Тема 1.22. Застосування диференціального числення функції кількох змінних
Локальний екстремум функції двох змінних та його дослідження. Умовний екстремум функції двох змінних і метод Лагранжа його дослідження. Моделі оптимізації задач економіки. Однорідні функції. Формула Тейлора. Опуклі функції.
Розділ 10. ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЇ ОДНІЄЇ І КІЛЬКОХ ЗМІННИХ
Тема 1.23. Невизначений інтеграл, його властивості та найпростіші методи обчислення
Первісна функції та невизначений інтеграл. Властивості невизначеного інтеграла. Таблиця невизначених інтегралів. Найпростіші методи обчислення невизначеного інтеграла: метод зведення до табличних на основі незалежності його від вибору змінної інтегрування, метод підстановки, метод інтегрування частинами. Застосування невизначеного інтеграла в економічному аналізі: загальні витрати, маргінальні витрати, середні витрати; загальний дохід, маргінальний дохід, середній дохід.
Тема 1.24. Визначений інтеграл, його властивості та обчислення
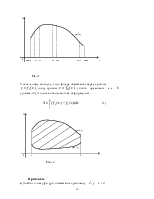
Поняття інтегральної суми і визначеного інтеграла. Геометричний та економічний зміст визначеного інтеграла. Властивості визначеного інтеграла. Формула Ньютона-Лейбніца обчислення визначеного інтеграла. Метод підстановки та інтегрування частинами у визначеному інтегралі. Поняття невласних інтегралів. Поняття кратних інтегралів.
Тема 1.25. Застосування визначеного інтеграла.
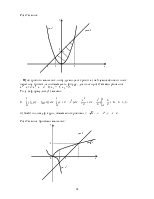
Обчислення площі криволінійної трапеції. Обчислення об’єму тіла обертання. Обчислення додаткового загального доходу. Нарощування капіталу. Прибуток від процентів вкладу. Споживче активне сальдо. Застосування невласних інтегралів у фінансах.
Розділ 11. ЧИСЛОВІ І ФУНКЦІОНАЛЬНІ РЯДИ
Тема 1.26. Числові ряди та їх збіжність
Поняття числового ряду та його суми. Необхідна умова збіжності числового ряду. Еталонні ряди: ряд геометричної прогресії і гармонійний ряд. Ознаки порівняння і Даламбера збіжності числового ряду з додатними членами. Знакопочерговий ряд (ряд Лейбніца) та умови його збіжності. Абсолютна та умовна збіжність знакозмінного ряду.
Тема 1.27. Функціональні ряди
Поняття функціонального ряду та області його збіжності. Рівномірна збіжність функціонального ряду та ознака Вейєрштрасса. Поняття степеневого ряду. Теорема Абеля і радіус збіжності степеневого ряду. Ряди Тейлора і Маклорена.
Розвинення функцій ![]() у степеневі
ряди. Формули Ейлера. Розвинення функцій
у степеневі
ряди. Формули Ейлера. Розвинення функцій ![]() у
степеневі ряди. Застосування степеневих рядів. Поняття ряду Фур’є.
у
степеневі ряди. Застосування степеневих рядів. Поняття ряду Фур’є.
Розділ 12. ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ
Тема 1.28. Диференціальні рівняння першого порядку
Поняття диференціального рівняння першого порядку, його частинного і загального розв'язку. Задача Коші. Диференціальні рівняння з відокремлюваними змінними. Однорідне диференціальне рівняння та зведення його до рівняння з відокремлюваними змінними. Лінійне диференціальне рівняння та його інтегрування методом варіації сталої. Застосування диференціальних рівнянь першого порядку в економічному аналізі: неоплачена модель зростання, модель природного зростання випуску, зростання випуску в умовах конкуренції, динаміка ринкових цін.
Тема 1.29. Лінійні диференціальні рівняння другого порядку
Поняття диференціального рівняння другого порядку та його частинного і загального розв’язків. Лінійне однорідне диференціальне рівняння другого порядку та властивості його розв’язків. Структура загального розв'язку лінійного однорідного диференціального рівняння другого порядку та його знаходження методом Ейлера у випадку рівняння зі сталими коефіцієнтами. Структура загального розв'язку лінійного неоднорідного диференціального рівняння 2-го порядку та його знаходження методом варіації сталих. Метод невизначених коефіцієнтів знаходження часткового розв'язку лінійного неоднорідного диференціального рівняння 2-го порядку зі сталими коефіцієнтами. Застосування диференціальних рівнянь 2-го порядку в економічному аналізі: модель ринку з прогнозованими цінами і т.п.
Тема 1.30. Лінійні різницеві рівняння
Оператор зсуву. Формули інтегрування Григорі-Ньютона. Різницеві методи Адамса чисельного інтегрування диференціальних рівнянь. Лінійні різницеві рівняння зі сталими коефіцієнтами (однорідні і неоднорідні). Застосування лінійних різницевих рівнянь в економічному аналізі: економічна модель розвитку Самюельсона–Хікса, павутинні моделі ринку, динамічна модель Леонтьєва.
Розділ 13. ЕЛЕМЕНТИ ФІНАНСОВОЇ МАТЕМАТИКИ І МАТЕМАТИЧНОЇ ЕКОНОМІКИ
Тема 1.31. Елементи фінансової математики
Прості і складні відсотки та обчислення нагромадження; Номінальна
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.