Временное и спектральное представление сигналов

Тема 1.4. Временное и спектральное представление сигналов

Формы представления сигналов

Существует две формы представления сигналов:

·  временная форма представления сигналов;

·  спектральная форма представления сигналов.

Временная форма представления сигнала – это описание изменения его параметров в функции времени. Такая форма описания позволяет определить энергию, мощность и длительность сигнала.

Временная форма может быть представлена:

·  математической моделью (аналитической записью);

·  временной диаграммой (осциллограммой) сигнала.

Следует отметить, что выбрать математическую модель для реального электрического сигнала не всегда просто. Для примера рассмотрим телефонный сигнал, реализации различных фрагментов которого приведены на рис. 1.4.1. Даже визуальный анализ этих временных диаграмм приводит к заключению, что совсем непросто подобрать функцию времени, которая точно совпадала бы, например, с временной диаграммой u(t) на всем интервале времени [0,Т]. Если бы такую функцию удалось найти, то, скорее всего, она была бы представлена достаточно сложным выражением. Поэтому можно сказать, что временные диаграммы телефонного сигнала имеют сложную форму.

Рисунок 1.4.1.

Практически все электрические сигналы, используемые в электросвязи для представления сообщений, имеют сложную форму. Это утверждение относится, в частности, к сигналам вещания, а также телевизионным, телеграфным сигналам и др.

Для исследования частотных свойств сигналов используется спектральное представление функции с помощью преобразования Фурье временной формы, когда в качестве простых функций выбирают гармонические колебания. Сущность этого представления состоит в следующем: любой электрический сигнал u(t) на произвольно заданном интервале времени длительностью Т от t = t₀ до t = t₀+T можно записать в виде суммы простых гармонических колебаний (ряда Фурье):

где

U₀ – постоянная составляющая, В;

U_mk – амплитуды гармоник, В;

ω₁ – частота первой гармоники, рад/с;

φ_к – начальная фаза k-й гармоники.

Спектральная форма представления сигнала – это представление параметров сигнала в виде двух графиков:

·  графика спектра амплитуд;

·  графика спектра фаз.

Спектральная диаграмма амплитуд показывает распределение энергии сигнала между составляющими его спектра. Пример такой диаграммы показан на рис. 1.4.2. Структура спектра периодического сигнала полностью определяется значениями амплитуд и фаз гармоник. Высота линий спектра амплитуд пропорциональна амплитуде данной гармоники, поэтому их высоты различны. Основание спектральной линии на оси частот лежит в точке, соответствующей частоте гармоники. Длины линий спектра фаз пропорциональны значению фаз. Основание спектральной линии на оси частот лежит в точке, соответствующей частоте гармоники.

Рисунок 1.4.2. График спектра амплитуд

Рисунок 1.4.3. График спектра фаз

Периодические сигналы и их спектры

Гармонический сигнал

Математическая модель сигнала:

u(t) = U_m*cos(ω₀*t+φ₀).

Параметрами гармонического сигнала являются:

·  u_m, – амплитуда, В;

·  ω₀ – угловая частота, рад/с;

·  φ₀ – начальная фаза, рад.

При построении графиков спектров более удобно угловую частоту ω₀, рад/с перевести в линейную f₀, Гц по формуле:

f₀ = ω₀/2*π

Рисунок 1.4.4. График спектра амплитуд

Рисунок 1.4.5. График спектра фаз

Вывод: гармонический сигнал имеет одну спектральную линию на графике спектра амплитуд и одну спектральную линию на графике спектра фаз.

Сложный периодический сигнал (бигармонический сигнал)

u(t) = U_m1*cos(ω₁*t+φ₁)+U_m2*cos(ω₂*t+φ₂)

Рисунок 1.4.6. График спектра амплитуд

Рисунок 1.4.7. График спектра фаз

Вывод: сложный периодический сигнал имеет дискретный спектр.

Последовательность прямоугольных импульсов

В связи с тем, что последовательность прямоугольных импульсов является периодическим сигналом, его математическая модель может быть представлена рядом Фурье:

Данный ряд бесконечный, а каналов с бесконечной шириной полосы спектра не существует, поэтому его необходимо ограничить. Энергия гармоник, частоты которых попадают на интервал от 0 до 4*π/t (t – длительность импульса), составляет около 95% энергии этого сигнала на одном периоде. Длина этого периода равна ширине первых двух лепестков, что составляет 2*q гармоник (q = Т/t – скважность).

В качестве примера рассмотрим последовательность прямоугольных импульсов со скважностью q = 3 и построим спектр первых двух лепестков:

Рисунок 1.4.8. График спектра амплитуд

Рисунок 1.4.9. График спектра фаз

Выводы:

·  последовательность прямоугольных импульсов имеет дискретный и бесконечный спектр;

·  гармоники, частоты которых кратны скважности, обращаются в ноль;

·  расстояние между линиями спектра равно частоте первой гармоники;

·  гармоники, входящие в состав нечетных лепестков, имеют фазу (+π/2), а гармоники, входящие в состав четных лепестков, имеют фазу (-π/2).

Примечание: формулы для расчета параметров спектра будут даны в практической работе.

Непериодические сигналы и их спектры

Сигналы, не являющиеся периодическими, называются непериодическими. К ним относятся многие реальные сигналы электросвязи. Гармонический анализ периодических сигналов можно распространить на непериодические сигналы, если представить непериодический сигнал как периодический, но с периодом, стремящимся к бесконечности (Т→∞).

Рисунок 1.4.10. а, б – прямоугольный импульс и его спектральная плотность; в, г – затухающий импульс и его спектральная плотность

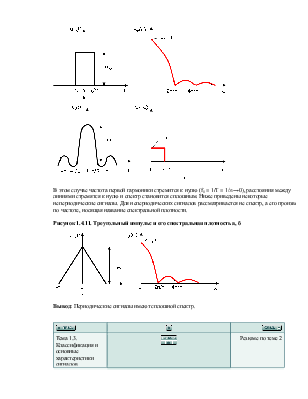
В этом случае частота первой гармоники стремится к нулю (f₁ = 1/T = 1/∞→0), расстояния между линиями стремятся к нулю и спектр становится сплошным. Ниже приведены некоторые непериодические сигналы. Для непериодических сигналов рассматривается не спектр, а его производная по частоте, носящая название спектральной плотности.

Рисунок 1.4.11. Треугольный импульс и его спектральная плотность а, б

Вывод: Периодические сигналы имеют сплошной спектр.