Расчет подкрановой балки. Сбор нагрузок. Определение расчетных усилий. Подбор сечения балки. Установление размеров опорной части балки с проверкой на устойчивость

2.4 Расчет подкрановой балки.

2.4.1 Сбор нагрузок.

Для крана грузоподъемностью Q=5т по ГОСТ 25546–82  принимаем:

P_к=55 кН – максимальное давление крана на рельс, G_т=20 кН – масса тележки, крановый рельс КР-70 по ГОСТ 4121-76*.

Вертикальное давление колеса крана:

, где:  – коэффициент сочетаний при учете работы одного крана;

 – коэффициент надежности по нагрузке;

 – коэффициент надежности по назначению здания;

 – коэффициент динамичности.

Горизонтальное боковое давление колеса крана от поперечного торможения тележки:

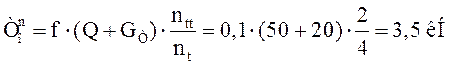, где:  – коэффициент трения при торможении тележки с гибким подвесом                                   груза;

 – вес тележки;

– число тормозных колес тележки;

– общее количество колес.

Нормативное горизонтальное усилие, передающееся одним колесом крана:

.

2.4.2 Определение расчетных усилий.

Для определения наибольших изгибающих моментов и поперечных сил устанавливаем краны в самое невыгодное положение. Положение равнодействующей сил R=2P_к по отношению к середине балки находим по значению x (рис.1а).

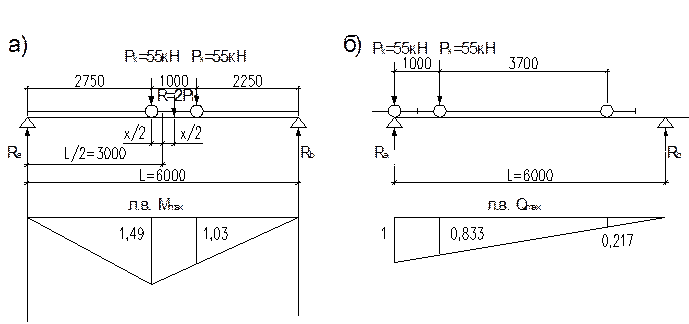
Рис. 2     Линии влияния  M_max и Q_max.

Опорные реакции:

,

.

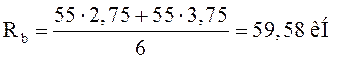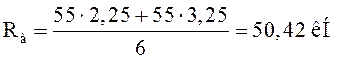Максимальные изгибающий момент и поперечная сила от вертикальной нагрузки определяются по ф-лам :

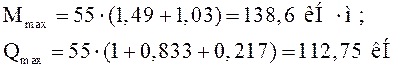
Расчетные изгибающий момент и поперечная сила с учетом собственного веса вычисляются следующим образом:

, где и  - коэф., равные :

,

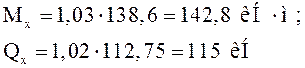
Расчетные изгибающий момент и поперечная сила от поперечной горизонтальной нагрузки:

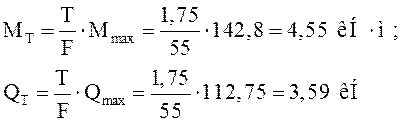
2.4.3 Подбор сечения балки.

По таблице 50 для конструкции II группы в климатическом районе II₄ принимаем сталь С235. По таблице 51 при толщине проката от 4 до 10 мм и св. 10 до 20 мм расчетное сопротивление листового проката R_y=230 МПа.

Определяем требуемый момент сопротивления балки:

.

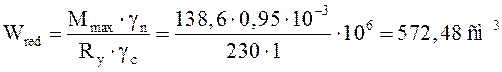Определяем минимальную высоту сечения балки из условия жесткости, т.е. не допущения предельного прогиба:

.

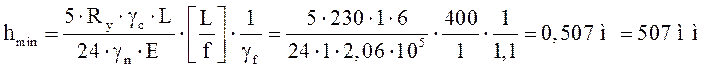Предварительно задавшись высотой балки 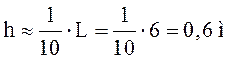, определим рациональную толщину стенки .

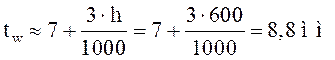Минимальная толщина стенки из условия ее работы на срез:

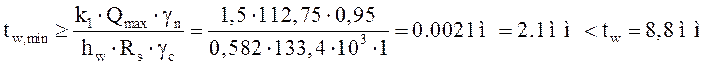, где: =1.5;

;

– высота стенки, принимаемая из условий:

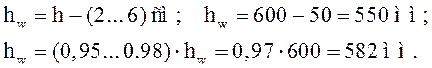
Определяем толщину стенки из условия смятия под колесом крана:

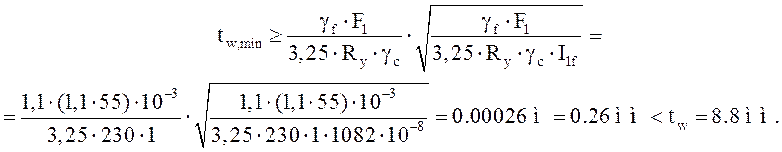
 – расчетное давление колеса крана с учетом коэффициента перегрузки n=1.1.

– момент инерции рельса.

Окончательно принимаем толщину стенки .

Определяем оптимальную высоту балки из условия минимального расхода материала для асимметричных балок:

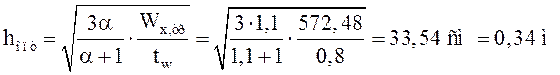, где:  – коэффициент асимметрии сечения.

Окончательно принимаем высоту балки h=350 мм.

Определяем требуемую площадь сечения составной балки, а также площади ее верхнего и нижнего поясов:

;

;

.

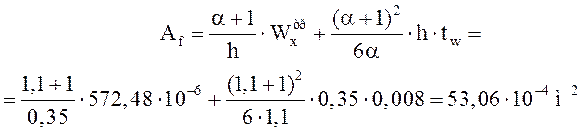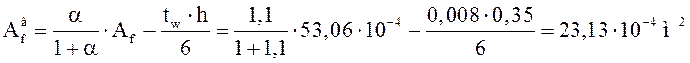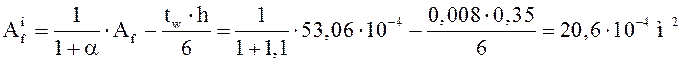Компонуем сечение исходя из следующих соображений:

1.  Из условия обеспечения общей устойчивости балки: ;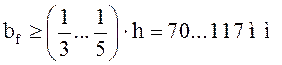

2.  Из условия свариваемости элементов: , принимаем  (по сортаменту ГОСТ 82-70*);

3.  Из условия обеспечения местной устойчивости сжатого пояса: ;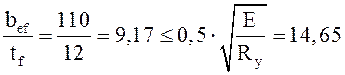

4.  ;

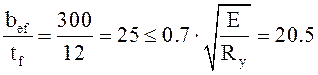5.  Назначаем  по сортаменту универсальной стали:  с учетом того, что минимальная ширина верхнего пояса должна быть не менее 300мм. Ширина нижнего пояса должна быть не менее 180мм, что гарантирует применение автоматической сварки. Принимаем ширину нижнего пояса .

С учетом полученных параметров принимаем  сечение балки (рис. 2).

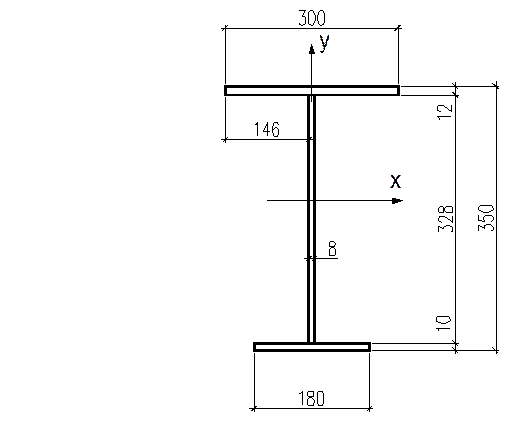
Рис. 2   Сечение подкрановой балки.

Геометрические характеристики принятого сечения балки.

Определим геометрические характеристики сечения с помощью программного комплекса «LIRA»

Х А Р А К Т Е Р И С Т И К И   С Е Ч Е Н И Я

	Наименование	Обозначение	Значение	Ед. изм.
	И С Х О Д Н Ы Е   Д А Н Н Ы Е
	Модуль упругости	E	23	кН/см2
	Коэффициент Пуассона	n	0.3
	Модуль сдвига	G	8.84615	кН/см2
	Плотность материала	r	7.69822e-005	кН/см3
	Я Д Р О В Ы Е   Р А С С Т О Я Н И Я
	Максимальная абсцисса	Y+	2.64822	см
	Минимальная абсцисса	Y-	2.64822	см
	Максимальная ордината	Z+	9.81386	см
	Минимальная ордината	Z-	15.1415	см
Наименование		Обозначение	Значение	Ед. изм.
Ж Е С Т К О С Т Н Ы Е   Х А Р А К Т Е Р И С Т И К И
Осевая жесткость		EF	1845.52	кН
Изгибная жесткость относительно оси Y		EIy	384619	кН*см2
Изгибная жесткость относительно оси Z		EIz	73310.1	кН*см2
Жесткость на кручение		GIt	0	кН*см2
Секториальная жесткость		EIw	0	кН*см4
Сдвиговая жесткость относительно оси Y		GFy	0	кН
Сдвиговая жесткость относительно оси Z		GFz	0	кН
Погонная масса		g	0.617705	кН
Г Е О М Е Т Р И Ч Е С К И Е   Х А Р А К Т Е Р И С Т И К И
Габариты сечения:		b	30	см
		h	35	см
Координаты центра тяжести относительно системы координат Xo0oYo:		Xoc	-8.445e-017	см
		Yoc	21.236	см
Периметр внешнего контура		Pext	164.4	см
Периметр внутренних контуров		Pint	0	см
Площадь		F	80.24	см2
Момент инерции относительно оси X		Ix	16722.6	см4
Момент инерции относительно оси Y		Iy	3187.4	см4
Центробежный момент инерции относительно системы координат XOY		Ixy	-8.47033e-014	см4
Угол поворота главных осей инерции		Fi	0	°
Главный момент инерции относительно оси Y		Iy	16722.6	см4
Главный радиус инерции относительно оси Y		Ry	14.4363	см
Главный момент инерции относительно оси Z		Iz	3187.4	см4
Главный радиус инерции относительно оси Z		Rz	6.30264	см
Момент сопротивления изгибу относительно оси Y (Z+)		Wy+	1214.95	см3
Момент сопротивления изгибу относительно оси Y (Z-)		Wy-	787.464	см3
Момент сопротивления изгибу относительно оси Z (Y+)		Wz+	212.493	см3
Момент сопротивления изгибу относительно оси Z (Y-)		Wz-	212.493	см3