Создание таблицы, рисунка в программе Microsoft Excel, страница 7

Для квадрата со стороной a периметр P можно вычислить с помощью следующих формул

Переходим к формулам для двух огородов в форме прямоугольников. Обозначим через b меньшую сторону прямоугольника, а через q отношение его сторон (для первого прямоугольника q=2, для второго – q=3). Тогда формулы для вычисления периметра в случае прямоугольника можно записать так

Рассмотрим теперь формулы для выбора самого короткого забора вокруг четырех огородов. Пусть i – порядковый номер огорода, P_i – периметр i - го огорода, P_min – искомый минимальный периметр. Тогда можно написать формулу

Обозначим буквой T – форму огорода с самым коротким забором и напишем формулу для ее автоматического вычисления

Легко проверить, что условия задачи позволяют выполнить расчеты по формулам (3.1)-(3.5) и найти решение поставленной задачи.

3.4. Описание решения задачи

Фрагмент рабочего листа Excel с решением задачи об огородах (см. рис. 3.1) дает пример возможного оформления результатов вычислений.

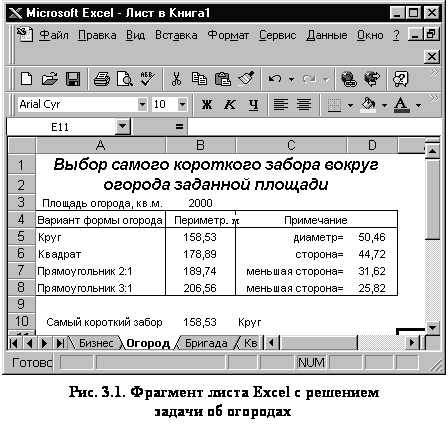Ввод и форматирование заголовка произведено так, как описано в задачах о платежной ведомости и об оптимальном бизнесе. Заданная площадь огородов введена в ячейку B3. Расчеты, связанные с определением длины заборов вокруг огородов, представлены в табличной форме в ячейках интервала A4:D8. Первая колонка таблицы представляет варианты формы огородов. Длина заборов (периметры), вычисленная по формулам (3.1)-(3.3), видна во втором столбце таблицы. Вспомогательные величины вычислены в ячейках интервала D5:D8 и вместе с кратким пояснением в ячейках C5:C8 образуют третий столбец таблицы (см. рис. 3.1). Например, для квадрата в ячейку D6 введена формула =КОРЕНЬ(B3), обеспечивающая вычисление стороны, а в ячейку B6 формула =4*D6 для вычисления периметра. Копирование этих формул в другие ячейки не производилось, поэтому в них можно использовать ссылки на ячейки любого типа. Основу указанных двух формул составляют формулы (3.2) из подраздела 3.3.

Наибольший интерес представляют формулы в ячейках B10 и C10. В ячейку B10 введена формула =МИН($B$5:$B$8), реализующая вычисление минимального периметра P_min по формуле (3.4). Более сложна формула в ячейке C10

=ЕСЛИ(B5=B10;A5;ЕСЛИ(B6=B10;A6;ЕСЛИ(B7=B10;A7;A8)))

Она реализует выбор варианта формы огорода с минимальным периметром в точном соответствии с формулой (3.5). Пояснения по использованию логической функции ЕСЛИ имеются в подразделе 2.4.

3.5. Выводы

Результаты решения задачи соответствуют известному математическому факту: чем более «правильную» форму имеет плоская фигура заданной площади, тем меньше ее периметр. Периметры огородов в форме круга, квадрата и двух прямоугольников (см. рис. 3.1) увеличиваются по мере уклонения их формы от «правильной». Наименьший периметр 158,53 м имеет огород в форме круга. Наибольший периметр 206,56 м у прямоугольника с отношением сторон 3:1. Следовательно, по сравнению с круглым огородом забор для второго прямоугольного огорода на 48,03 м длиннее. Соответственно увеличиваются затраты на его строительство.

На практике круглые огороды не очень распространены. Поэтому из трех других вариантов формы следует выбрать квадрат, у которого периметр меньше, чем у остальных.