





МО РБ
УО «ПОЛОЦКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Кафедра “Сопротивления материалов
Строительной механики”
РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА №1
“Динамический расчёт плоской стержневой системы на действие вибрационной нагрузки”
Выполнил студент гр.03-ПГС-1: Кезик Ю.И.
Проверил : Родионов В. К.
НОВОПОЛОЦК 2006
ВАРИАНТ №12.
Строка №6.
Для данной стержневой системы определить собственные частоты свободных колебаний и динамические внутренние усилия при действии динамической нагрузки.
Материал балки – сталь Ст.3., модуль упругости ![]()
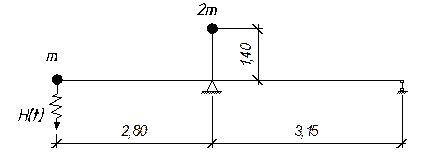
Дано:
![]()
![]()
![]()
![]()
![]()
![]()
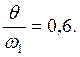
Решение:
1. Кинематический анализ.
А) Изобразим расчётную схему балки в виде кинематической цепи.

Б) Подсчитаем число степеней свободы.
![]()
![]()
Вывод: Система может быть геометрически неизменяема и статически определима.
В) Анализ геометрической структуры.
Диск Д1 крепится к диску “Земля” при помощи – не параллельных, не пересекающихся в одной точке стержней, и образует единый жёсткий диск.
Вывод: Система является геометрически неизменяемой и статически определимой.
2. Определение собственных частот и построение собственных форм свободных колебаний системы.
2.1 Определим полное и неполное число степеней свободы.
![]()
![]()
2.2 Изобразим систему в деформированном состоянии и наложим на систему параметры при помощи которых определяется положение колеблющихся масс в любой момент времени.
2.3 Изобразим основную систему обратного метода (рис. 1в).
2.4 Составим дифференциальное уравнение свободных колебаний системы в обратной форме:
![]()
![]()
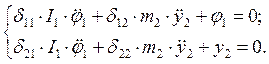 (1)
(1)
2.5 Решаем систему дифференциальных уравнений свободных колебаний и получаем систему амплитудных уравнений:
![]()
![]() (2)
(2)
![]()
![]()
Подставим 2 в 1 и получаем:
![]()
![]()
Данная система уравнений является системой линейных однородных алгебраических уравнений.
Система имеет два решения:
1. ![]()
![]() Колебаний нет.
Колебаний нет.
2. ![]()
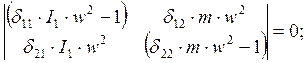 (3)
(3)
2.6
Определим величину ![]() , для чего рассмотрим основную
систему обратного метода в двух единичных состояниях, и построим единичные
эпюры, а затем по формуле
, для чего рассмотрим основную
систему обратного метода в двух единичных состояниях, и построим единичные
эпюры, а затем по формуле 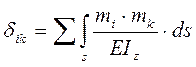 определяем величину
этих коэффициентов
определяем величину
этих коэффициентов
Состояние
![]() (рис. 1г)
(рис. 1г)
Состояние
![]() (рис. 1д)
(рис. 1д)
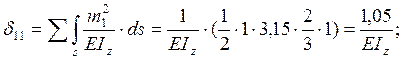
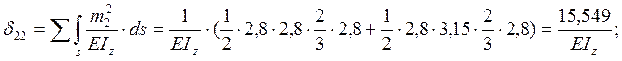
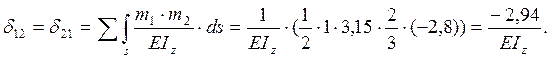
2.7
Подставляем найденные коэффициенты ![]() и
и ![]() в (3) , преобразовываем его и раскрываем,
в результате чего получаем преобразованное частотное уравнение.
в (3) , преобразовываем его и раскрываем,
в результате чего получаем преобразованное частотное уравнение.
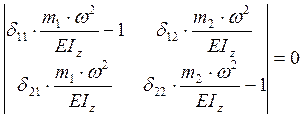 , умножим строку на
величину
, умножим строку на
величину 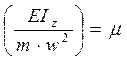 .
.
Получаем 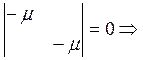
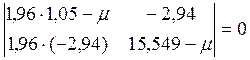
![]()
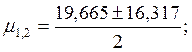
![]()
![]()
2.8 Определим требуемый № двутавра из условия её статической прочности на изгиб.
![]()
![]()
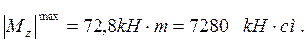 (рис. 1з).
(рис. 1з).
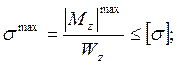
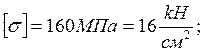
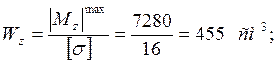 По полученным
параметрам из сортамента прокатной стали, выбираем двутавр Ι № 30.
По полученным
параметрам из сортамента прокатной стали, выбираем двутавр Ι № 30. ![]()
![]()
определим 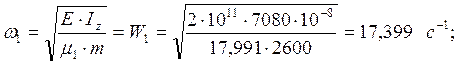
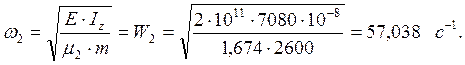
2.9 Строим спектр собственных частот в безразмерной форме.
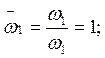
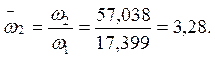
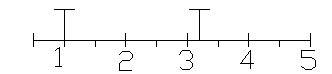
2.10 Построим собственные формы свободных колебаний. Для чего используем преобразованное амплитудное уравнение.
![]()
А) форма с ![]()
![]()
Пусть ![]() тогда
тогда ![]()
Б) форма с ![]()
![]()
Пусть ![]() тогда
тогда ![]()
На основании выполненных расчетов построим собственные формы свободных колебаний системы (рис. 1е,ж).
2.11 Проверим ортогональность собственных форм.
![]()
![]()
![]()
2.12 Определяем нормирующие множители для первой и второй собственных форм.
![]() ;
;
1 форма
![]()
2 форма
![]()
Значения ортонормированных амплитуд:
1 форма 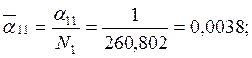
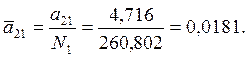
2 форма 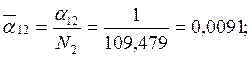
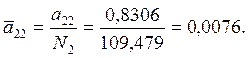
Правильность нахождения ортонормированных амплитуд:
![]()
![]()
3. Динамический расчёт системы на вибрационную нагрузку:
M=2600кг.
![]() ; H=2,6кН;
; H=2,6кН;
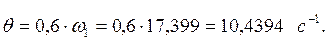
3.1 Составим дифференциальные уравнения вынужденных колебаний в обратной форме:
![]()
![]()
![]()
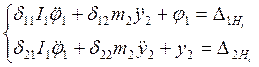
Система однородных Д.У.
При установившемся режиме будем искать в форме частных уравнений:
![]()
![]()
![]()
![]()
![]()
![]()
После преобразований получим:
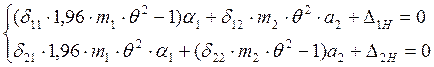
![]() Преобразуем амплитудные
уравнения вынужденных колебаний в систему уравнений амплитудных значений сил
инерций;
Преобразуем амплитудные
уравнения вынужденных колебаний в систему уравнений амплитудных значений сил
инерций;
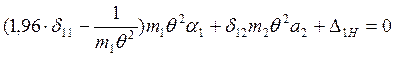
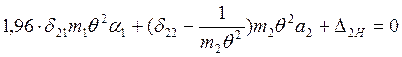
После преобразований получим:
![]()
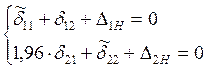
Коэффициенты
![]() определяются так же, как и при расчёте на
свободные колебания.
определяются так же, как и при расчёте на
свободные колебания.
Определяем
величину ![]() и
и ![]() :
:
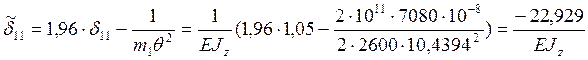
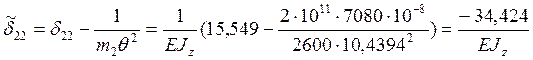
Для
определения свободных членов ![]() и
и ![]() рассмотрим О.С.
обратного метода на действие амплитудного значения возмущающей нагрузки (рис.
1и)
рассмотрим О.С.
обратного метода на действие амплитудного значения возмущающей нагрузки (рис.
1и)
По формуле :
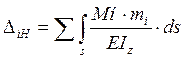 определим
величину свободных членов:
определим
величину свободных членов:
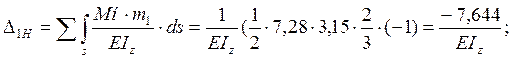
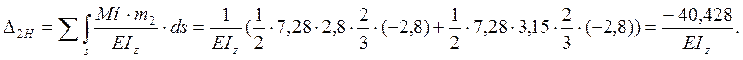
Решаем систему амплитудных значений и определяем их величину:
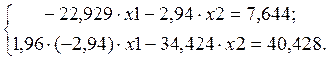
x1=-0,187; x2=-1,143.
Строим
эпюры ![]() (рис. 1к,л).
(рис. 1к,л).
Строим
эпюру ![]() (рис. 1м).
(рис. 1м).
![]()
Строим
полную эпюру динамических усилий ![]() (рис. 1н).
(рис. 1н).
![]()
Определяем амплитуды:
![]()
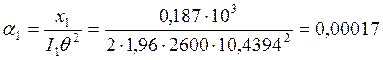 рад.
рад.
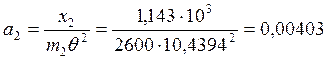 м.
м.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.