Ac=2hf’beff+bw0.9d=2*43,45мм*1460мм+458мм*0.9*7*159=206080,9мм
Центр тяжести сечения: y0=h/2=230/2=115мм
Момент инерции сечения.
Заменим приведенное сечение на следующее:
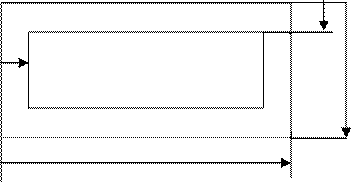
Ic=(beff*h3/12)+(0.9dn0.93d3)/12=
=(1460*2303)/12+(0.9*159*7*0.93*1593)/12=
=1235707702мм4
Момент сопротивления сечения относительно нижней грани:
Wc=Ic/y0=1235707702мм4 /115=10745284мм3
Приведенное сечение:
Ared=Ac+Asp*αp
αp = Es/ Ecm=200МПа/27МПа=7,4
Ared=206080,9мм2 + 1231мм2*7,4=215190,3 мм2
Sred = 2*( beff - bw)* hf’*( h- hf’/2)+h2*bw/2+ 2*( beff - bw)* hf’2/2+Ap*c* αp
Sred = 2*(1460-458)*43.45*(230-43.45/2)+43.452*458/2+2*(1460-458)*43.452/2+ 1231*7,4*20=30475120.6мм3
y0= yred= Sred/ Ared=30475120.6мм3/215190,3 мм2=141.6мм
Ired=2* beff hf’3/12+ beff hf’(h- hf’/2- yred)2+ beff hf’(-hf’/2+ yred)2+ bw (h- 2hf’)3/12+ bw (h- 2hf’)(h/2- yred)2+ Ap (- yred +c) αp=1699074779мм4
2.2 Расчет потерь предварительного напряжения
2.2.1 Потери предварительного напряжения от релаксации арматуры:
∆Pir=(0.1σ0,max - 20)Asp=(0.1*609.5МПа-20)*1231мм=50409Н
2.2.2 Потери от деформации анкеров:
∆PA=(∆l/l)Es*Asp= (2мм/6200мм)*2*105МПа*1231мм=79419Н
l -длина натягиваемого стержня, l=6200мм
∆l-обжатие спрессованных шайб, ∆l=2мм
2.2.3.Потери вызванные деформацией стальной формы
∆Pf=30* Asp=30*1231мм=36930Н
2.2.4 Усилие обжатия:
P0 = σ0,max * Asp =609,5МПа*1231мм=750295Н
2.2.5. Потери предварительного напряжения в результате упругих деформаций бетона
∆Pc=α*ρp(1+(Zcp2*Ac)/Ic)Po.c=7.4*0.006(1+(882*206080,9)/1235707702)*583537=29267Н
Где Ρp=Asp/Ac=1231мм/206080,9=0.006
αp=Es/Ecm=(2*105)/(27*103)=7.4
Zcp - расстояние от точки приложения усилия предварительного обжатия до центра тяжести бетонного сечения, Zcp=230мм/2-20мм-7мм=88мм
Ро.с - усилие предварительного напряжения с учетом потерь, реализованных к моменту обжатия бетона,
P0.c= P0 -Pir-∆PA ∆Pf =750295-50409-79419-36930=583537Н
Усилие предварительного обжатия к моменту времени t=to, действующее после отдачи усилия предварительного обжатия на конструкцию
Pm.0=P0.c-∆Pc=696.73-59.857=636.87кН≤0.75FpkAsp=763,2кН
2.2.6 Реалогические потери предварительного напряжения, вызванные усадкой, ползучестью бетона и длительной релаксацией напряжения в арматуре
∆Рt(t)=∆σp,c+s+1Asp
∆σp.c+s+r=(εcs(t,to)*Es+∆σpr+α*Ф(t,to)*(σcp+σcp0))/(1+α*Asp/Ac*(1+Ac/Ic*Zcp2)*(1+0,8*Ф(t,to)))
Где εcs – относительные деформации полной усадки бетона в произвольный момент времени t
εcs(t,to)= εcsd(t,to)+ εcs,a=-0.00053
где εcsd(t,to) – относительная деформация физической усадки бетона в момент времени t, обусловленная высыханием. Для бетона С12/15 εcsd(t,to)=0,455*10-3
εcs,a – относительная деформация химической и суточной усадки, обусловленной процессами твердения вяжущих
εcs,a=βas(t)*εcs,a(∞), где βas(t)= 1-2,71(-0.2*t^0.5)=0.86, t=100 дней
εcs,a(∞)=-2,5*(fck-10)*10-6=-2.5*(12-10)*10-6=--0.000005
εcs,a=0.86*(-0.000005)=-4.3*10-6
Ф(t,t0) – коэффициент ползучести бетона для периода времени от t0 до t, зависящий от h0
h0=2Ac/U=2*206080,9мм/3454мм=119,3ммм,
Где U периметр сечения плиты U=3454мм,
Ф(t,t0)=2.7
σcp – напряжение в бетоне на уровне центра тяжести напрягаемой арматуры от практически постоянной комбинации нагрузок, включая собственный вес
σсp= Mp*Zcp/Ic=60,96*106*88/1235707702=4,34МПа
σсро=(Pmo/Ac)+(Pmo*Zcp2/Ic)= 554270/206080,9+ 554270*882/1235707702=6,16МПа где, σсро – начальное напряжение в бетоне на уровне центра тяжести напрягаемой арматуры от действия усилия предварительного обжатия,
∆σpr – изменение напряжений в напрягаемой арматуре в расчетном сечении, вызванное релаксацией арматуры
∆σpr=0.03σ0,max=0.03*609,5МПа=18.3МПа
∆σp.c+s+r=(0.00053*2*105МПа+18.3МПа+7,4*2.7*(-4,34+6,16))
/(1+7.4*1231/206080,9*(1+206080,9*882/1235707702)*(1+0.8*2.7))=141МПа
∆Pt(t)=141МПа*1231мм2=173571Н
Среднее значение усилия предварительного обжатия Рm,t в момент времени t>t0
Рm,t= Pmo-∆Pt(t)
Рm,t=554270Н-173571Н=380699Н < 0.65*fpk*Ap=0.65*800МПа*1231мм2=640120Н
Рm,t=380699Н<P0-100*Ap=627195Н
2.3 Расчет плиты по образованию трещин, нормальных к продольной оси.
Расчетная ширина раскрытия трещин, нормальных к продольной оси.
Расчетная ширина раскрытия трещин, нормальных к продольной оси цемента, определяется по формуле:
Wk=β*Srm*εsm<=Wlim=0.2мм где, β – коэффициент, учитывающий отношение расчетной ширины раскрытия трещин к средней, при расчете ширины раскрытия нормальных трещин, образующихся от усилий, вызванных соответствующей комбинацией нагрузок (частная) β=1.7
Srm – среднее расстояние между трещинами
εsm – средние деформации арматуры определяемые при соответствующей комбинации нагрузок, εsm=1
Mcr – момент, соответствующий образованию трещин
Mcr=(fctm+σcpo)*Wc
где, fctm=1.6*106Па
Mcr=10745284мм3*(1,6МПа+6,16МПа)=83,38кН*м
Mfk=66,6кН*м
Т.к. Mcr> Mfk, то из этого следует, что трещины не образуются при данной величине нагрузок и расчет величины раскрытия трещин производить нет необходимости.
2.4 Расчет прогибов ж/б плиты, работающей без трещин
Для наиболее характерных расчетных схем ж/б элементов и способов нагружения, применяемых в практике проектирования максимальный прогиб может быть определен по формуле:
a(∞,t0)=αk* Mpk*leff2/(Ec,eff*Ired)+ αk Npd*Zcp*leff2/(Ec,eff*Ic)<=alim
αk - коэффициент, зависящий от условий закрепления и нагружения плиты
Ired – приведенный момент инерции сечения
Ec,eff= - эффективный модуль упругости, определяемый с учетом ползучести бетона по формуле:
Ec,eff=Ecm/(1+Ф(t,to))=7.3*103МПа
Npd=0.9* Рm,t=0.9*380699Н=342629.1H
Zcp=88мм
αk = 5/48
αp = 1/8
a(∞,t0)= 5/48* 60.96*103Нм*57602/(7,3*103МПа*1699074779мм4)+ 342629.1H *88мм*57602/( 8*7.3*103МПа *1235707702мм4)=13,84мм
l –пролет плиты, l=5900мм
alim – предельно допустимый прогиб, установленный нормативным документом
alim= l/198.33= 29.7мм
a(∞,t0)= 13,84мм< alim=29.7мм условие выполняется.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.