Расчет сборной железобетонной многопустотной панели перекрытия. Расчет сборного железобетонного марша

Найдем предельное отклонение предварительного напряжения при числе напрягаемых стержней  n=4, по формуле:

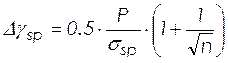,                                                                (2.10)

.

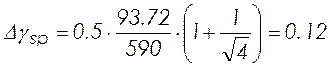Коэффициент точности натяжения :

,                                                                                  (2.11)

.

При проверке по образованию трещин в верхней зоне плиты обжатии принимаем:

.

Предварительное напряжение с учетом точности натяжения:

,                                                                                         (2.12)

МПа.

Окончательное предварительное натяжение арматуры с учетом  min-го значения суммарных потерь  МПа определяется

 МПа

2.1.7 Расчет прочности плиты по сечению, нормальному к продольной оси.

( кН×м)

Расчетное сечение представляет балку таврового сечения полкой в сжатой зоне.

Вычисляем :

                                                                         (2.13)

тогда ;

Находим высоту сжатой зоны

                                                                                                 (2.14)

 см – нейтральная ось проходит в пределах сжатой зоны.

Характеристика сжатой зоны

Граничная высота сжатой зоны

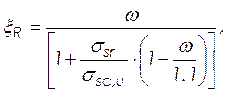                                                                  (2.15)

,

 МПа

 МПа,  так как

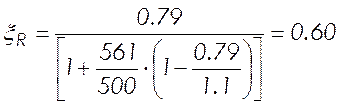
Коэффициент условий работы, учитывающий сопротивление напрягаемой арматуры выше условного предела текучести определяют по формуле:

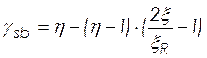                                                                     (2.16)

где  – для арматуры класса А-V.

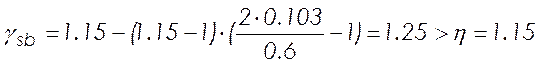
Принимаем .

Определяем площадь поперечного сечения рабочей предварительно напряженной арматуры по формуле:

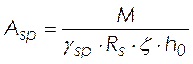,                                                                                          (2.17)

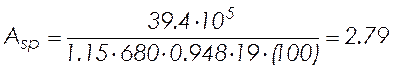 см²

Принимаем из конструктивных соображений  4Æ12 Ат-V с площадью см².

2.1.8 Расчет прочности плиты по сечению, наклонному к продольной оси

Расчетная поперечная сила

 кН

Определяем усилие обжатия бетона

,                                                                                            (2.18)

 кН

Влияние усилия при наличии предварительного напряженной продольной арматуры, расположенной в растянутой зоне:

                                                                      (2.19)

Проверяем требуется ли поперечная арматура по расчету:

                                                                                                  (2.20)

НН

условие выполняется.

                                                                                 (2.21)

где  – проекция наклонного сечения, м;

, если выполняется условие:

,

гдекН/м<кН/м

условие выполняется, следовательно

 см.

                                                                                    (2.22)

 Н,

 Н – условие выполнятся.

Следовательно, поперечной арматуры по расчету не потребуется.

На приопорных участках длиной  l/4 арматуру устанавливаем конструктивно,

принимаем Æ4 Вр-I с шагом S=h/2.

S=220/2=110 мм, принимаем S=200 мм.

2.1.9 Определение геометрических характеристик приведенного сечения для расчета плиты по предельным состояниям второй группы.

Площадь приведенного сечения:

 см².

Расстояние от нижней грани до центра тяжести приведенного сечения

 см.

Момент инерции сечения

 см⁴

Момент сопротивления сечения

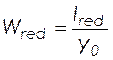 ,                                                                                                      (2.23)

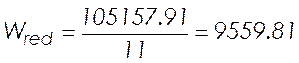 см³.

Расстояние от ядровой точки, наиболее удаленной от растянутой зоны, до центра тяжести и тоже наименее удаленной от растянутой зоны:

                                                                                     (2.24)

где                                                                           (2.25)

 см.

Упругопластический момент сопротивления по растянутой зоне

                                                                                                      (2.26)

где  для двутаврового сечения;

 см³.

2.1.10 Потери предварительного напряжения арматуры

Предварительное напряжение в арматуре без учета потерь принимаем

МПа

Определяем первые потери:

– от релаксации напряжений в арматуре

,                                                                                                     (2.27)

 МПа.

– от температурного перепада , так как при пропаривании форма нагревается вместе с панелью;

– при деформации бетона от быстро натекающей ползучести.

Усилие обжатия

,                                                                          (2.28)

 кН.

Эксцентриситеты усилия  относительно центра тяжести приведенного сечения:

,                                                                                                            (2.29)

где  – толщина защитного слоя, м.

 см.

Напряжение в бетоне при обжатии:

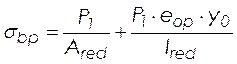,                                                                                  (2.30)

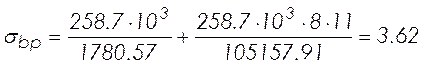 МПа

Устанавливаем значение передаточной прочности бетона из условия:

,

 МПа МПа.

Принимаем  МПа.

Тогда отношение

Вычисляем сжимающие напряжения в бетоне на уровне центра тяжести площади напрягаемой арматуры от усилия обжатия

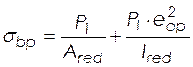                                                                                           (2.31)

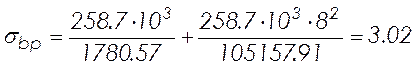 МПа

при ,

где                                                                                     (2.32)

 следовательно потери от быстро натекающей ползучести:

;                                                             (2.33)

где:;

МПа.

Усилие обжатия с учетом первых потерь:

кН,

Напряжение в бетоне при обжатии

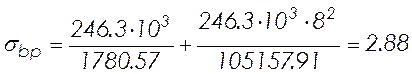 МПа.

Определяем вторые потери

– от усадки бетона

МПа;

– от ползучести бетона

,                                                                               (2.34)

МПа

Суммарное значение вторых потерь:

 МПа

Суммарные потери

 МПа МПа.

Принимаем значение всех потерь МПа.

Усилие обжатия с учетом всех потерь

 кН.

2.1.11 Расчет по образованию трещин, нормальных к продольной оси

Коэффициент надежности по нагрузке .

Расчетный момент от полной нормативной нагрузки кН×м.

Должно соблюдаться условие

,                                                                                                          (2.35)

где  – момент внутренних усилий.

,                                                                                     (2.36)

где                                                                                   (2.37)

 кН×см.

 кН×м;

 кН×м кН×м, следовательно, трещины в растянутой зоне не образуются.

Проверим образуются ли трещины в верхней сжатой зоне плиты.

Расчетное условие:

,                                                                              (2.38)

где  МПа – сопротивление бетона растяжению, соответствующее передаточной прочности бетона МПа.

931999 Нсм < 1433971 Нсм

условие выполняется, трещины не образуются. Расчет на раскрытие трещин не производится.

2.1.12 Расчет прогиба плиты

Прогиб в середине пролета плиты при отсутствии трещин в растянутой зоне определяем по значению кривизны :

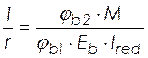,                                                                                                 (2.39)

где  – коэффициент, учитывающий снижение жесткости под влиянием неупругих деформаций бетона в растянутой зоне ();

  – при действии кратковременной нагрузки;

  – при действии постоянных и длительных нагрузок;

Кривизна плиты с учетом действия усилия предварительного обжатия:

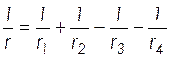,                                                                                   (2.40)

а полный прогиб соответственно:

,                                                                           (2.41)

Определяем значение кривизны и прогибов:

– от действия кратковременной нагрузки

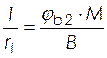,                                                                                                        (2.42)

где – жесткость, Н×см²

,                                                                                        (2.43)

Н×см²;

;

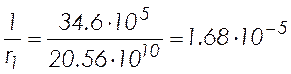
– от действия полной нагрузки

;

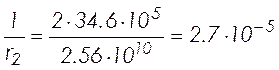
– влияние кратковременной ползучести;

– кривизна, обусловленная выгибом элемента от кратковременного действия усилия обжатия  с учетом всех потерь

;

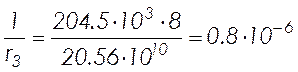
– кривизна, обусловленная выгибом под влиянием ползучести и от усилия предварительного обжатия

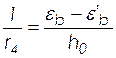,                                                                                                       (2.44)

где  и  – деформации бетона, вызванные ползучестью, на уровне центра тяжести растянутой арматуры и крайнего сжатого волокна бетона;

;

;

;

;

.

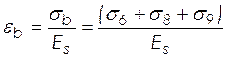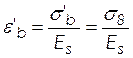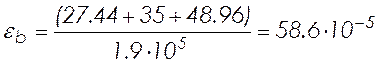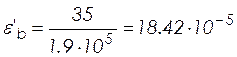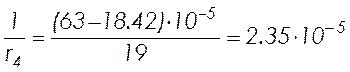
Соответственно прогибы

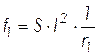,                                                                                                          (2.45)

где  – коэффициент, учитывающий схему и вид нагрузки.

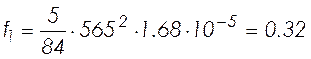см;

,

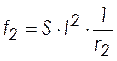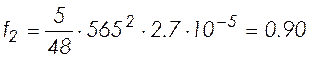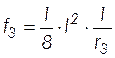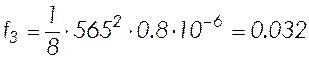 см;

;

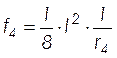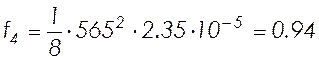 см;

;

 см;

Полный прогиб

 см.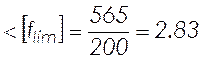

см  см.

Следовательно, принятое сечение плиты и армирование удовлетворяет требованиям расчета по I и II группам предельных состояний.

2.1.13 Проверка панели на монтажные усилия

Монтажные петли располагаются на расстоянии  см от торцов панели.

Расчетная нагрузка от собственного веса панели:

                                                                        (2.46)

где  – приведенная толщина плиты,  см.

 – плотность тяжелого бетона кг/м³.

 – конструктивная ширина панели, м

 – коэффициент динамичности

Н/м.

Расчетная схема панели имеет вид, показанный на рисунке 2.3.

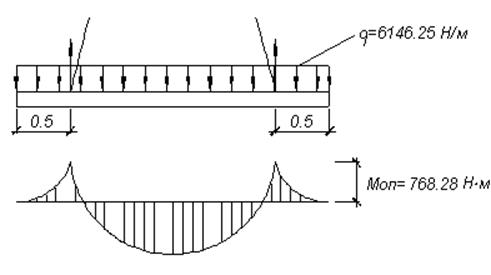
Рисунок 2.4 – Расчетная схема панели при монтаже

Величина отрицательного изгибающего момента от веса консольной части панели

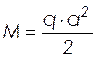,                                                                                                (2.47)

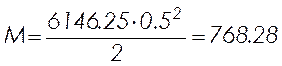 Н×м.

Этот момент воспринимается продольной арматурой верхней сетки С-1 и конструктивной продольной арматурой каркасов К-1. В верхней сетки в продольном направлении расположены 8 стержней  Æ4 Вр-1 с шагом 200 мм. Площадь поперечного сечения этих стержней:

см²;

Необходимое количество арматуры на восприятие отрицательного момента:

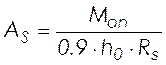,                                                                                              (2.48)

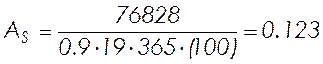 см².

что значительно меньше имеющейся арматуры  см².

Прочность панели на монтажные усилия обеспечена.

2.1.14 Расчет монтажных петель

Определяем нагрузку от собственного веса панели:

,                                                                                                             (2.49)

.

Здесь  – вес 1 погонного метра панели.

Усилие на одну петлю, при условии передачи нагрузки от панели на 3 петли

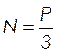,                                                                                             (2.50)

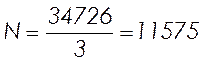 Н.

Определяем площадь поперечного сечения одной петли из стали класса А-I.

МПа, (табл. СНиП 2.03.01-84)

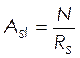,                                                                                                             (2.51)

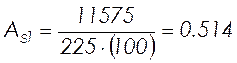см².

Принимаем конструктивно петлю Æ12 A-Iсм².

2.2 Расчет сборного железобетонного марша

Необходимо рассчитать и сконструировать железобетонный марш шириной 1,35 м для лестничной клетки.

Высота этажа 3,3 м.

Угол наклона марша  a = 30°, ступени размером 15 х 30 см.

Бетон класса В25, арматура каркасов класса А-III, сеток В_р-I.

2.2.1 Определение нагрузок и усилий

qⁿ=3,6 kH/м².

Коэффициент надежности  g_f = 1,2.

Длительно действующая временная нагрузка: рⁿ= 1,2 кH/м².

Расчетная нагрузка на 1 м длины марша:

q = (qⁿg_f + pⁿg_f)f,                                                                                              (2.52)

q = (3,6*1,1 + 3*1,2)*1,35 = 10,21 кH/м.

Расчетный изгибающий момент в середине пролета марша:

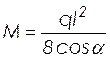,                                                                                    (2.53)

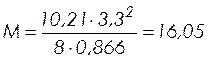кНм.

Поперечная сила на опоре:

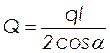,                                                                                    (2.54)

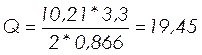кН.

2.2.2 Предварительное назначение размеров сечения марша

Толщина плиты по сечению между ступенями h¹_f = 30 мм, высота ребер (косоуров)  h = 170 мм, толщина ребер В_R = 80 мм.

Действительное сечение марша заменяем на расчетное тавровое с полкой в сжатой зоне:

В = 2В_R = 2•80 = 160 мм; ширина полки В¹_f при отсутствии поперечных ребер принимается не более:

В¹_f = 2•(l/6) + В = 2•(330/6) + 16 = 126 см, или

В¹_f = 12h¹_f + В = 12•3 + 16 = 52 см.

Принимаем за расчетное меньшее из 2-х значений: В¹_f = 52 см.

2.2.3 Подбор площади сечения продольной арматуры

Устанавливаем расчетный случай для таврового сечения

(при х = h _f) при   М £R_в•g_в•В¹_f•h¹_f • (h_o – 0,5•h¹_f);

1605000 < 14,5• (100) •0,9•52•3• (14,5 – 0,5•3) = 2646540 Н•см.

Условие удовлетворяется, нейтральная ось проходит в полке:

a_m= 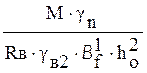,                                                                                (2.55)

a_m=.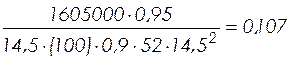

по таблице  z=0,944; x=0,112.

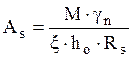,                                                                                                    (2.56)

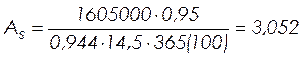 см².

Принимаем   2Æ14 АIIIcA_s = 3,08 см².

В каждом ребре устанавливаем по одному каркасу К-1.

2.2.4 Расчет наклонного сечения на поперечную силу

Поперечная сила на опоре Q_max = 19,45•0,95 = 18,48 кH.

Вычисляем проекцию расчетного наклонного сечения на продольную ось с:

В_в = j_в2• (1 + j_f + j_n) •R_вt•g_в2 В•h²_о,                                                                 (2.57)

где j_n = 0;

j_f = 2•0,75• (3•h¹_f) •h¹_f/В•h_o,                                                                          (2.58)

j_f = 2•0,75• (3•3) •3/16•14,5 = 0,175 < 0,5.

1 + j_f + j_n = 1 + 0,175 + 0 = 1,175 < 1,5.

В_в = 2• (1 + 0,175 + 0) •1,05•0,9• (100) •16•14,5² = 7,5•10⁵ Н/см.

В расчетном наклонном сечении :

Q_в = Q_sw = Q/2,  а т.к по формулам Q_в = В_в/2, то

В_в/0,5•Q = 7,5•10⁵/0,5•18480 = 81,17 см, что больше 2•h_o = 29 см.

Тогда Q_в = В_в/c = 7,5•10⁵/29 = 25,9•10³ H = 25,9 кH, что больше Q_max=18,48кH, значит, поперечная арматура по расчету не требуется. Назначаем из конструктивных соображений поперечные стержни   Æ6  мм из стали класса АI с шагом S = 80 мм, не более  h/2 = 170/2 = 85 мм, А_sw = 0,283; R_sw = 175 МПа, для двух каркасов n=2; А_sw = 0,566 см²; m = 0,566/16,8 = 0,0044; a=E_s/E_в=2,0•10⁵/2,7•10³= 7,4.

В средней части ребер поперечную арматуру располагаем конструктивно с шагом 200 мм.

Проверяем прочность элемента по наклонной полосе между наклонными трещинами:

Q£ 0,3j_w1•j_в1 •R_d •g_в2 •В•h_o,

где j_w1 = 1 + 5am_w,                                                                                          (2.59)

j_w1 = 1 + 5am_w = 1 + 5•7,4•0,0044 = 1,16;

j_в1 = 1– 0,01•14,5•0,9 = 0,87.

Q = 18480 < 0,3•1,16•0,87•14,5•0,9•16•14,5• (100) =91664 H–условие соблюдается, прочность марша по наклонному сечению обеспечена.

2.2.5 Расчет по деформациям

Изгибающий момент в середине пролета:

от полной нагрузки: qⁿ= 3600•1,35 = 4860 H/м;

pⁿ = 3000•1,35 = 4050 H/м;

Мⁿ = (4860 + 4050) •3,3² • 0,95/8 = 11522