Известно,
что 
. Тогда 
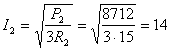А.
Начальную фазу для тока фазы А принимаем = 0.
А, 
А, 
А.
4. Определение фазных напряжений для 3-ей и 2-ой нагрузки.
В соответствии с законом Ома
В.
В, 
В.
Поскольку нагрузки 2 и 3 соединены параллельно, напряжения на их фазах равны
В, 
В, 
В.
5. Определение линейного тока для 2-ой нагрузки.
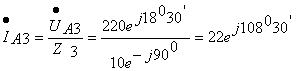
А,
А.
6.
Определение суммарного тока 
для 2-ой и 3-ей
нагрузки.
По
первому закону Кирхгофа 
Величину
этого тока можно определить другим способом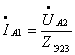 
,
где
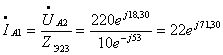A, 
A, 
A
7.Определение эквивалентного сопротивления всей схемы.
Ом
8. Определение фазного напряжения на входе схемы.
В
В, 
В
9. Определение линейных напряжений на входе схемы.
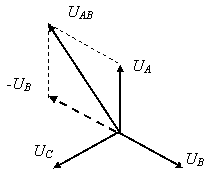Из векторной диаграммы, изображенной на
рисунке, при равномерной (симметричной) нагрузке, следует 
.
Таким образом, линейные напряжения на входе схемы определяются
В.
В. 
В.
Аналогично определяются линейные напряжения на нагрузке
В.
В. 
В.
10. Определение фазных токов на 2-ой нагрузке.
Найденный ранее ток 2-ой нагрузки для схемы соединений Y является фазным и одновременно – линейным, поскольку для Y Iф = Iл .
Чтобы определить истинные токи в фазах 2-ой нагрузки, соединенных в схему D, воспользуемся известными соотношениями
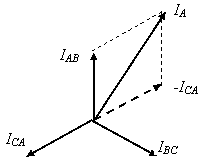Из схемы соединений D
.
.
.
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.