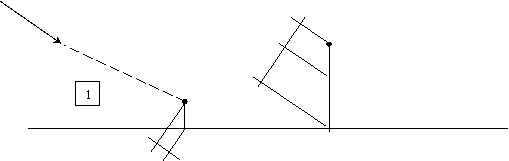
Под действием
внешних сил Р1 и Р2 первый стержень
удлинится на величину Δl1, а второй – укоротится на величину Δl2,
при этом жёсткая балка AD повернётся в положение
AD1. Ввиду малости упругих деформаций
горизонтальными смещениями точек B, C и D, лежащих на оси
балки, можно пренебречь, и будем считать, что эти точки в ходе деформирования
системы переместятся вертикально и займут положение B1,
C1 и D1
соответственно. Положение этих точек определим пересечением линии AD1 и перпендикуляров, проведённых к
первоначальному направлению осевой линии балки AD
в точки B, C
и D. Удлинение первого стержня и укорачивание
второго находим графически: из точек В и С опускаем перпендикуляры
на линии О1В1 и О2С1,
соответствующие новым положениям стержней 1 и 2 после приложения
внешних нагрузок. Получим: 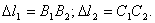
Составим
условие совместности деформаций.
ΔВВ1В2:
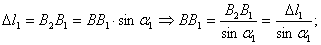
ΔСС1С2:
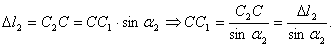

Условие совместности деформаций для заданной стержневой
системы:
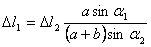 ,
,
примем 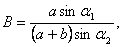 получим
получим
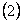

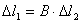 ,
где В – безразмерный коэффициент, учитывающий особенности геометрической
конфигурации системы.
,
где В – безразмерный коэффициент, учитывающий особенности геометрической
конфигурации системы.
Воспользуемся законом Гука для каждого из стержней 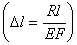 , из уравнения (2) получим
, из уравнения (2) получим 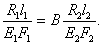 Учитывая
Учитывая 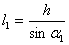 и
и
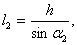 последнее соотношение будет иметь
вид:
последнее соотношение будет иметь
вид:
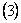
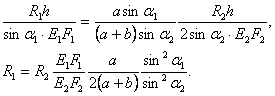
Решаем совместно систему уравнений (1) и (3):


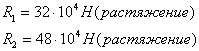
Проверим найденные численные значения, подставив их в уравнение (1):
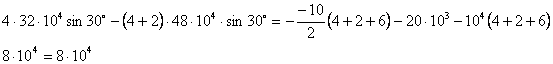
II. ОПРЕДЕЛЕНИЕ МОНТАЖНЫХ НАПРЯЖЕНИЙ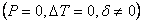 .
.
Второй стержень изготовлен с неточностью по длине 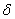 , т.е. с фактической длиной несколько
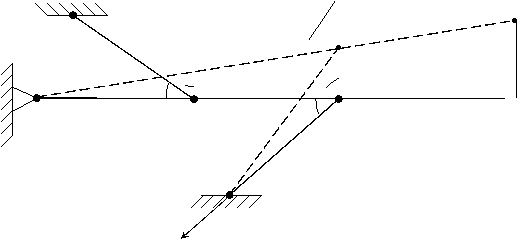
большей номинальной. Тогда при сборке в стержнях появятся внутренние
напряжения. Расчётная схема при этом будет выглядеть следующим образом:
, т.е. с фактической длиной несколько
большей номинальной. Тогда при сборке в стержнях появятся внутренние
напряжения. Расчётная схема при этом будет выглядеть следующим образом:
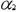
![]()
![]()
![]()

![]() ,
,![]() получим
получим![]()
![]()
![]() ,
где В – безразмерный коэффициент, учитывающий особенности геометрической
конфигурации системы.
,
где В – безразмерный коэффициент, учитывающий особенности геометрической
конфигурации системы.![]() , из уравнения (2) получим
, из уравнения (2) получим ![]() Учитывая
Учитывая ![]() и
и
![]() последнее соотношение будет иметь
вид:
последнее соотношение будет иметь
вид:![]()
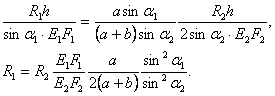


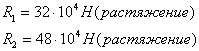
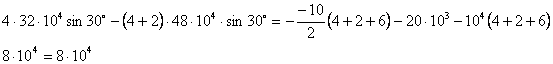
![]() .
.![]() , т.е. с фактической длиной несколько
большей номинальной. Тогда при сборке в стержнях появятся внутренние
напряжения. Расчётная схема при этом будет выглядеть следующим образом:
, т.е. с фактической длиной несколько
большей номинальной. Тогда при сборке в стержнях появятся внутренние
напряжения. Расчётная схема при этом будет выглядеть следующим образом: