Плоская стенка первоначально
прогрета равномерно до температуры ![]() .
.
В дальнейшем на внутренней
поверхности стенки ![]() обеспечивается условие
теплоизоляции (плотность теплового потока равна нулю), а с наружной
поверхностью
обеспечивается условие
теплоизоляции (плотность теплового потока равна нулю), а с наружной
поверхностью ![]() идет теплообмен с внешней средой, имеющей
постоянную температуру
идет теплообмен с внешней средой, имеющей
постоянную температуру ![]() . Толщина стенки
. Толщина стенки ![]() , коэффициент теплоотдачи
, коэффициент теплоотдачи ![]() . Изменение температуры в стенке
осуществляется в результате процесса теплопроводности.
. Изменение температуры в стенке
осуществляется в результате процесса теплопроводности.
Необходимо:
Получить временную зависимость температуры на внутренней поверхности стенки.
2.1. Решение.
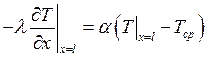 ;
;
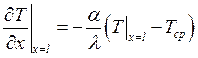 .
.
Заменив размерную координату на безразмерную, получим:
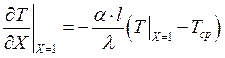 .
.
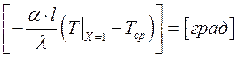 .
Заменим:
.
Заменим: 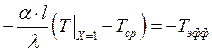 ;
;
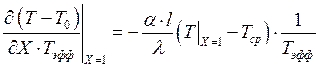 ;
;
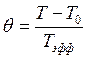 .
.
Поскольку все необходимые переменные мы привели к безразмерному виду, НУ и ГУ перепишутся следующим образом:
НУ: ![]() ;
;
ГУ: 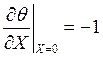 ,
,
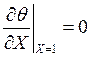 .
.
Отсюда:
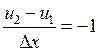 ,
,
![]() ,
, ![]() ,
, ![]() .
.
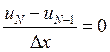 ,
,
![]() ,
, ![]() ,
, ![]() .
.
3. Лабораторная работа №3.
Постановка задачи:
Одна из поверхностей
металлической пластины толщиной ![]() нагревается постоянным
тепловым потоком
нагревается постоянным
тепловым потоком ![]() . Вторая поверхность
теплоизолирована. Температура пластины до нагрева составляла
. Вторая поверхность
теплоизолирована. Температура пластины до нагрева составляла ![]() .
.
Необходимо:
Для теплоизолированной поверхности построить зависимость температуры от времени и определить температуру на поверхности через 30 секунд от начала нагрева.
3.1. Решение.
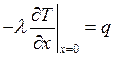 ;
;
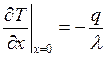 .
.
Заменив размерную координату на безразмерную, получим:
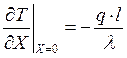 .
.
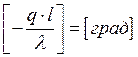 .
Заменим:
.
Заменим: 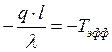 ;
;
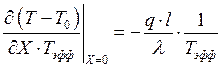 ;
;
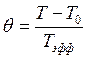 .
.
Поскольку все необходимые переменные мы привели к безразмерному виду, НУ и ГУ перепишутся следующим образом:
НУ: ![]() ;
;
ГУ: 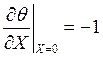 ,
,
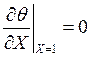 .
.
Отсюда:
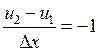 ,
,
![]() ,
, ![]() ,
, ![]() .
.
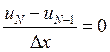 ,
,
![]() ,
, ![]() ,
, ![]() .
.
4. Лабораторная работа №4.
Постановка задачи:
Неограниченная плита
первоначально имеет однородную температуру ![]() . В
дальнейшем с одной стороны
. В
дальнейшем с одной стороны ![]() плита нагревается
тепловым потоком, плотность которого изменяется со временем по закону:
плита нагревается
тепловым потоком, плотность которого изменяется со временем по закону: ![]() , где
, где ![]() . Со
второй поверхности плиты обеспечивается условие теплоизоляции (плотность
теплового потока равна нулю). Толщина плиты
. Со
второй поверхности плиты обеспечивается условие теплоизоляции (плотность
теплового потока равна нулю). Толщина плиты ![]() .
Изменение температуры внутри плиты осуществляется в результате процесса
теплопроводностию
.
Изменение температуры внутри плиты осуществляется в результате процесса
теплопроводностию
Необходимо:
Получить временную зависимость температуры на расстоянии 21см от нагреваемой поверхности плиты.
4.1. Решение.
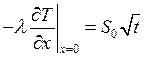 ;
;
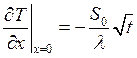 .
.
Заменив размерные величины на безразмерные, получим:
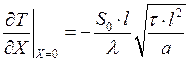 .
.
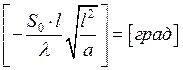 .
Заменим:
.
Заменим: 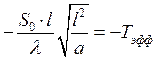 ;
;
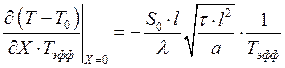 ;
;
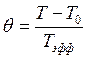 .
.
Поскольку все необходимые переменные мы привели к безразмерному виду, НУ и ГУ перепишутся следующим образом:
НУ: ![]() ;
;
ГУ: 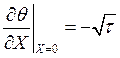 ,
,
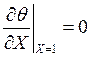 .
.
Отсюда:
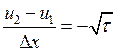 ,
,
![]() ,
, ![]() ,
, ![]() .
.
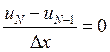 ,
,
![]() ,
, ![]() ,
, ![]() .
.
5. Лабораторная работа №5.
Постановка задачи:
Стальную плиту, нагретую
первоначально до 100˚С, нагревают с одной стороны тепловым потоком,
плотность которого меняется во времени с постоянной скоростью ![]() . Толщина плиты
. Толщина плиты ![]() . Потери
тепла с другой стороны плиты пренебрежимо малы.
. Потери
тепла с другой стороны плиты пренебрежимо малы.
Необходимо:
Найти зависимость температуры от времени (график) на расстоянии 2см от нагреваемой поверхности плиты и определить температуру через 15 минут.
5.1. Решение.
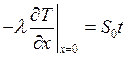 ;
;
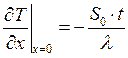 .
.
Заменив размерные величины на безразмерные, получим:
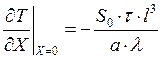 .
.
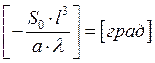 .
Заменим:
.
Заменим: 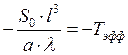 ;
;
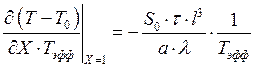 ;
;
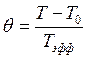 .
.
Поскольку все необходимые переменные мы привели к безразмерному виду, НУ и ГУ перепишутся следующим образом:
НУ: ![]() ;
;
ГУ: 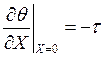 ,
,
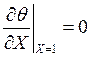 .
.
Отсюда:
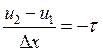 ,
,
![]() ,
, ![]() ,
, ![]() .
.
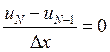 ,
,
![]() ,
, ![]() ,
, ![]() .
.
6. Лабораторная работа №6.
Постановка задачи:
Свинцовый лист толщиной 40см
первоначально прогретый до температуры ![]() ,
помещают в холодильную камеру, температура воздуха в которой уменьшается с
постоянной скоростью
,
помещают в холодильную камеру, температура воздуха в которой уменьшается с
постоянной скоростью ![]() от начальной температуры, равной
от начальной температуры, равной
![]() . Одна поверхность пластины
теплоизолирована, с другой происходит теплоотдача в камеру с коэффициентом теплоотдачи
. Одна поверхность пластины
теплоизолирована, с другой происходит теплоотдача в камеру с коэффициентом теплоотдачи
![]() .
.
Необходимо:
Построить графики зависимости температуры от
времени для трех плоскостей: ![]() ,
, ![]() ,
, ![]() .
.
6.1. Решение.
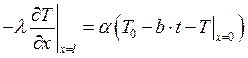 ;
;
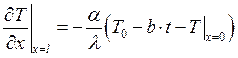 .
.
Заменив размерные величины на безразмерные, получим:
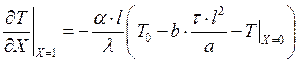 .
.
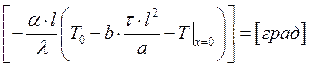 .
Заменим:
.
Заменим: 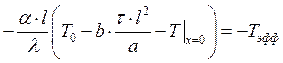
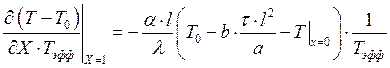 .
.
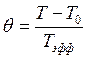 .
.
Поскольку все необходимые переменные мы привели к безразмерному виду, НУ и ГУ перепишутся следующим образом:
НУ: ![]() ;
;
ГУ: 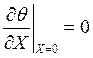 ,
,
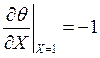 .
.
Отсюда:
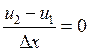 ,
,
![]() ,
, ![]() ,
, ![]() .
.
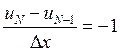 ,
,
![]() ,
, ![]() ,
, ![]() .
.
7. Результаты расчета.
7.1. Лабораторная работа №1.
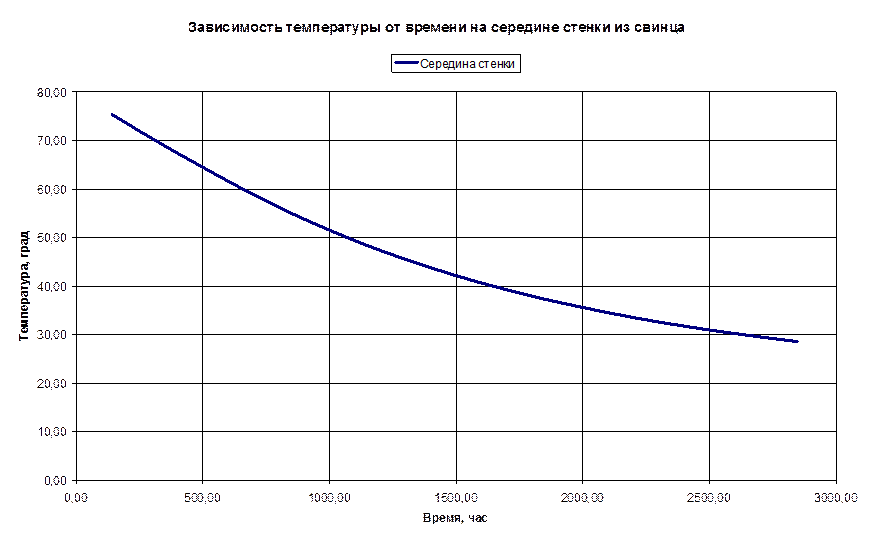
7.2. Лабораторная работа №2.
7.3. Лабораторная работа №3.
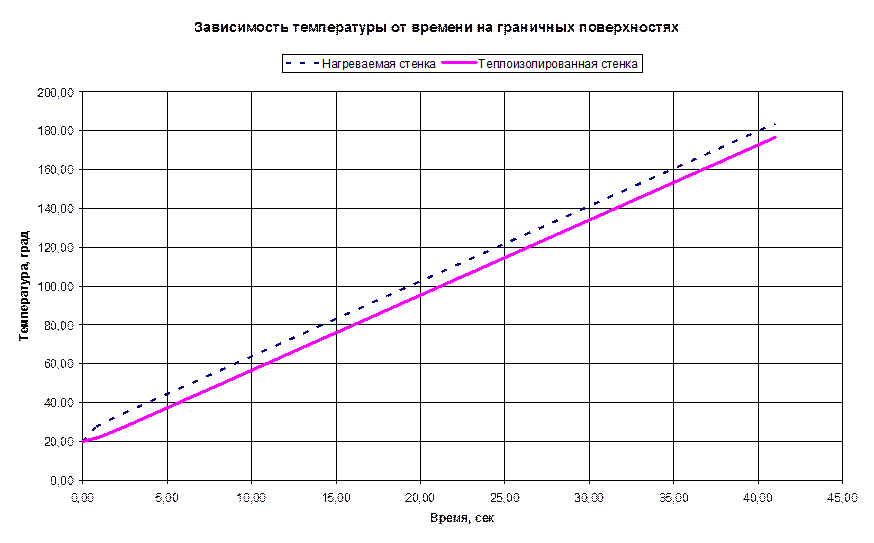
В результате расчета через 30 секунд после начала нагрева
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.