Синтез конечного автомата Мили. Программная реализация автомата

Министерство общего и профессионального образования Российской Федерации

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра РП РПУ

Проектирование элементов ЭВУ

Пояснительная записка к курсовой работе по дисциплине “Цифровые устройства и микропроцессоры”

Проверил:                                    Составил:

  преподаватель                              студент гр.         РТ5-03

_____________  (Сажнев А.М.)   _____________  Березовский П.А.

(подпись)                                        (подпись)

_____________                              _____________

(дата)                                              (дата)

Новосибирск

1998

Содержание курсовой работы

1.  Введение

2.  Задание

3.  Синтез конечного автомата Мили

a.  Построение графа конечного автомата

b.  Определение количество элементов памяти

c.  Составление таблицы переходов и выходов конечного автомата

d.  Составление таблицы возбуждения элементов памяти

e.  Синтез комбинационной части конечного автомата

f.  Реализация конечного автомата на микросхемах.

g.  Составление полной логической схемы автомата

Программная реализация автомата

Задание на курсовую работу

1  Синтезировать граф конечного автомата Мили

1.1  Построить граф конечного автомата для заданного варианта.

1.2  Определение структурной схемы автомата Мили (тип элемента памяти задан)

1.3  Составить таблицы переходов и выходов конечного автомата.

1.4  Составить таблицу возбуждения элементов памяти.

1.5  Синтезировать комбинационную часть конечного автомата.

1.6  Реализовать конечный автомат на микросхемах одной из серий: К155, К176, К351, К555, К561, К564. Составить полную логическую схему автомата.

2  Программная реализация автомата

2.1  Путем Эквивалентного преобразования исходного автомата Мили в автомат Мура построить граф и таблицу переходов автомата Мура.

2.2.   Составить схему алгоритма и программу, реализующую автомат Мура на языке ассемблера микропроцессора К580. Каждую команду программы сопроводить четкими комментариями, поясняющими смысл выполняемых действий.

1.  Синтезировать граф конечного автомата Мили

1.1  Построить граф конечного автомата для  варианта №21.

Имея обобщенный граф автомата с четырьмя внутренними состояниями, составим граф для заданного варианта. Для этого необходимо оставить только необходимые ветви обобщенного графа (рис.1), которые указаны в задании (табл.1).

Табл. 1 Нумерация внутренних состояний

Необходимо для каждой ветви графа, выходящей из вершины, сформировать комбинацию Z_iW_j  в строго определенном порядке и указать ее на графе.

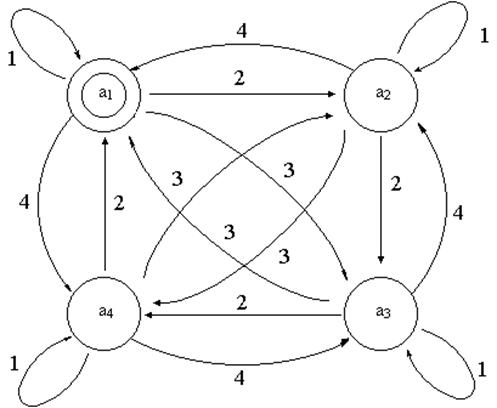
Рис. 1 Обобщенный граф автомата

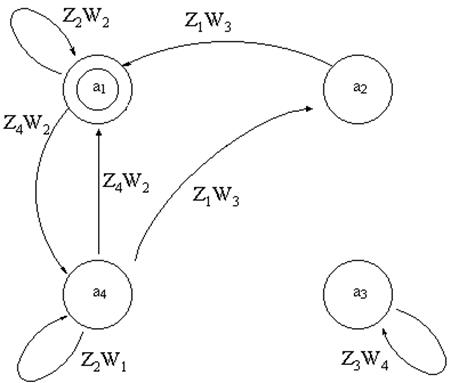
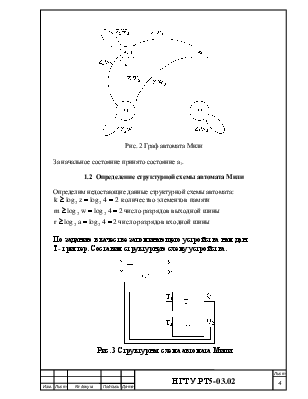
Рис. 2 Граф автомата Мили

За начальное состояние принято состояние а₁.

1.2  Определение структурной схемы автомата Мили

Определим недостающие данные структурной схемы автомата:

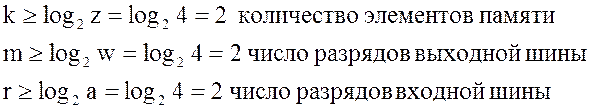
По заданию в качестве запоминающего устройства нам дан             Т- триггер. Составим структурную схему устройства.

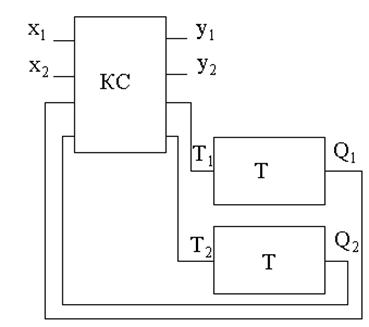
Рис. 3 Структурная схема автомата Мили

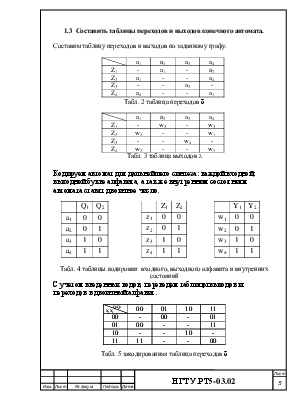
1.3  Составить таблицы переходов и выходов конечного автомата.

Составим таблицу переходов и выходов по заданному графу.

Табл. 2 таблица переходов d

Табл. 3 таблица выходов l

Кодируем автомат для дальнейшего синтеза: каждой входной, выходной букве алфавита, а так же внутренним состояниям автомата ставят двоичное число. 

Табл. 4 таблицы кодировки  входного, выходного алфавита и внутренних состояний

С учетом введенных кодов, переведем таблицы выходов и переходов в двоичный алфавит.

Табл. 5 закодированная таблица переходов d

Табл. 6 закодированная таблица выходов l

1.4 Составить таблицу возбуждения элементов памяти

Как уже отмечалось, в нашем автомате используются синхронные Т-триггеры (счетные триггеры). Его таблица истинности представлена в Табл.7. Для составления таблицы возбуждения памяти необходимо так преобразовать таблицу переходов автомата, так чтобы она показывала, какие сигналы необходимо подать на входы триггеров, чтобы перевести триггер в нужное состояние.

Табл. 7 Таблица переходов синхронного Т-триггера

Составим таблицу возбуждения памяти:

Табл. 8 Таблица возбуждения памяти

1.5  Синтез комбинационной части конечного автомата

По таблице возбуждения памяти составим систему уравнений, которая будет связывать входные сигналы памяти с внутренними состояниями и входными сигналами.

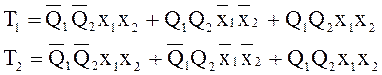  (1)

Минимизируем систему уравнений (1) при помощи карт Карно. Каждый бит (0-1) характеризует один триггер, по этому необходимо составить карты Карно для каждого триггера в отдельности (см. табл. 9,10).

Табл. 9 Карта Карно для первого        Табл. 10    Карта Карно для триггера                                        второго триггера

Наименьшая цена будет при минимизации “по единицам”.

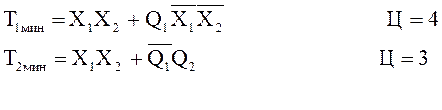    (2)   

По кодированной таблице выходов (табл. 6) составить логические уравнения сигналов на каждом информационном входе (табл. 11, 12).

Табл.  11                                         Табл. 12

Самой компактной будет минимизация по единицам.

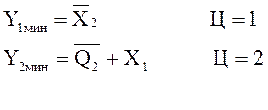 (3)

1.6  Реализовать конечный автомат на микросхемах одной из серий: К155, К176, К351, К555, К561, К564. Составить полную логическую схему автомата.

По логическим уравнениям (1) и (3) составим комбинационную часть в произвольном базисе, т.к., скажем, в базисе И-НЕ получается примерно в два раза больше корпусов.

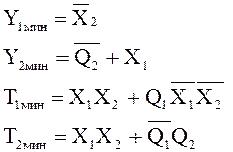
Реализуем автомат на микросхемах серии К555. Очевидно, что обязательно потребуются 2 триггера, а также логические элементы (И, ИЛИ, НЕ). Составим следующую таблицу.

Табл.13  Используемые микросхемы

Ниже приведем условное обозначение элементов:

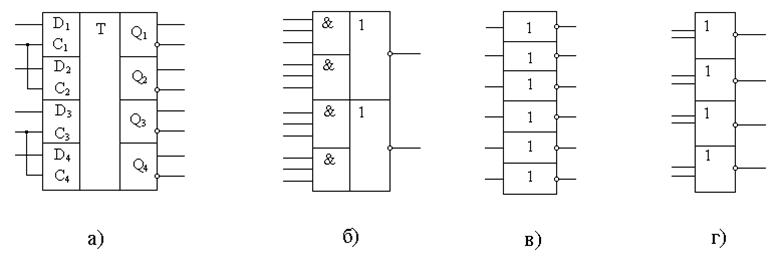
Рис. 4 Условное обозначение элементов

 a) К555ТМ1 б) К555ЛЕ1 в) К555ЛН1 г) К555ЛР11

Для реализации автомата нам необходимо всего лишь 4 корпуса.

Представим полную логическую схему автомата:

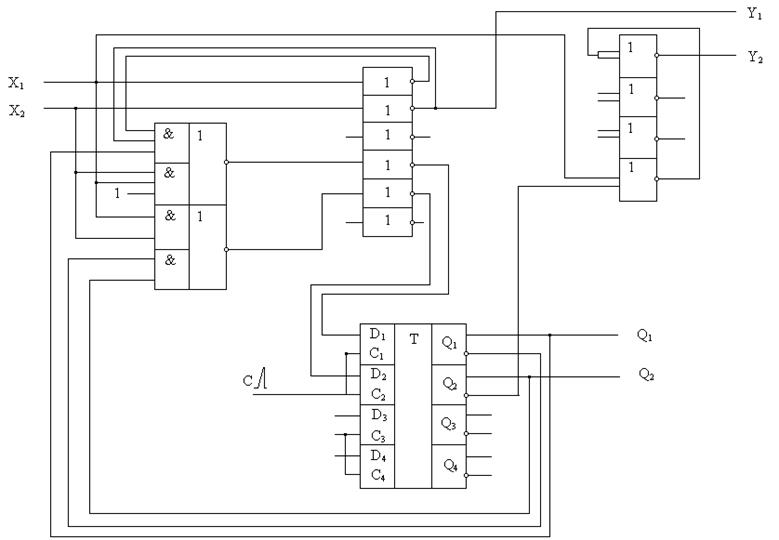
Рис. 5 логическая схема автомата

2.  Программная реализация автомата

2.1  Путем Эквивалентного преобразования исходного автомата Мили в автомат Мура построить граф и таблицу переходов автомата Мура

1.  Определим число двоичных разрядов, необходимых для представления кодов внутренних состояний, входных и выходных сигналов:

а) Количество двоичных разрядов, необходимое для кодирования всех входных сигналов:

б) Внутренних состояний (выходных сигналов):

2.  Кодируем автомат:

Таблица 14. Коды входных сигналов

Таблица 15 кодировка автомата

Теперь переведем таблицу переходов и выходов автомата в двоичный алфавит (Табл 16):

Таблица 16 Таблица переходов автомата Мура

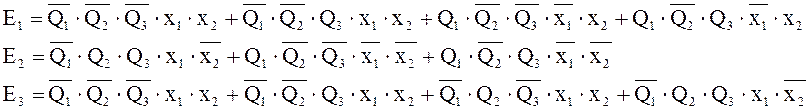3.  Обозначим  внутренне состояния автомата в последующем такте, как   и составляем для них логические уравнения «по единицам». Пусть характерезует  левый бит, - средний, а -правый. Составим ФАЛ (4).

(4)

Минимизирем выражения ,  и  .

a) Минимизируем E₁:

б) Минимизируем E₂:

в) Минимизируем E₃:

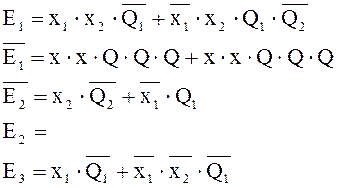
4.  Принимаем, что входные выходные сигналы и внутренние состояния