Расчет статически неопределимой системы в условиях работы составляющих ее элементов в режиме растяжения-сжатия (одноосное напряженное состояние), страница 2

Составим уравнения статики:

       (2)

или

            .                       (3)

Остальные уравнения статики можно не составлять, так как они необходимы лишь при определении реакций в шарнире X_A,Y_A, чего не требуется по условию задачи. Таким образом, степень статической неопределимости системы К=1, так как мы имеем два неизвестных усилия N₁, N₂ и одно уравнение равновесия статики.

            Для составления одного уравнения совместности деформаций необходимо рассмотреть схему перемещений системы. Под действием внешних сил Р₁ и Р₂ первый стержень удлинится на величину , а второй – на величину , при этом жесткая балка AD повернется в положение AD₁. Ввиду малости упругих деформаций горизонтальными смещениями точек B и C  в ходе деформирования системы переместится строго вертикально и займут положение В₁ и С₁. Положение этих точек определяется пересечением линий AD и перпендикуляров, проведенных к первоначальному направлению осевой линии балки AD в точки В и С.

            Удлинения и  находим также графически, для чего из точек В и С опустим перпендикуляры на линии О₁В₁ и О₂С₁, соответствующие новым положениям стержней 1 и 2 после приложения нагрузки Р. Отрезки В₁В₂ и С₁С₂ определяют удлинения соответственно и .

            Уравнения совместимости деформаций в данном случае проще всего составить, воспользовавшись подобием треугольников АВВ₁ и АСС₁:

                                                           .                                                      (4)

Из треугольников ВВ₁В₂ и СС₁С₂ определим

                                                 (5)

Подставив равенства (5) в формулу (4), получим уравнение совместности деформаций заданной стержневой системы

                                                                                              (6)

или , где

безразмерный коэффициент, учитывающий особенности геометрической конфигурации системы. Используя закон Гука для каждого из стержней

                                   ,

из уравнения (6) получим

                                               .

Учитывая, что ;  (рис.1), последнее соотношение можно переписать следующим образом:

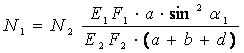                                                                                (7)

Далее решаем совместно систему уравнений (3) и (7):

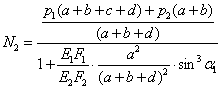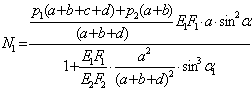;                      (8)

Из выражений (8) при известном отношении F₁/F₂ находим численные значения усилии:

                                   N₁=H (растяжение)