Достаточное условие заключается в положительности всех диагональных определителей матрицы Гурвица для данной системы. Для нашей системы (четвертого порядка) матрица будет иметь размерность 4´4, и иметь вид:
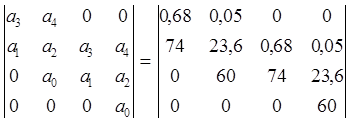
Таким образом, в нашем случае необходимое условие устойчивости, это положительность всех диагональных определителей:
,
,
,
.
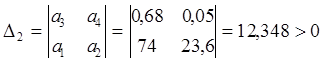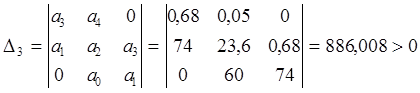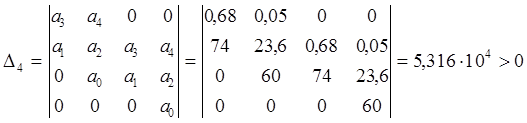Как мы видим из расчета, достаточное условие
устойчивости выполняется. В литературе также дается выражение для более
простого определения устойчивости системы по критерию Гурвица: 
. Подставив в это выражение наши коэффициенты получаем:
. Как мы видим - это условие устойчивости
также выполняется. Значит система устойчива.
8. Исследовать устойчивость системы по критерию Михайлова. Построить годограф.
Исследование устойчивости системы по критерию Михайлова (метод чередующихся корней) заключается в отыскании корней мнимой и реальной частей характеристического уравнения системы (G(p)), при условии p=jw . Характеристическое уравнение G(p) найдено нами в пункте 6. Подставим в него вместопеременной p - jw.
Запишем отдельно реальную и мнимую части G(jw):
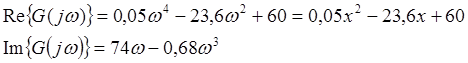, где
x=w2.
Определим значения x, при которых Re{G(jw)}=0:
x1=2,5562; x2=469,4438; w1=1,6; w1=21,667.
Определим значения w, при которых Im{G(jw)}=0:
w1=0; w2=10,432.
Разместим полученные корни в порядке возрастания:
w1=0, w2=1,6, w3=10,432, w4=21,667. (Корни Re{G(jw)} - подчеркнуты).
Так как корни действительной и мнимой частей чередуются, то, согласно критерию Михайлова, данная система устойчива.
Построим годограф Михайлова:
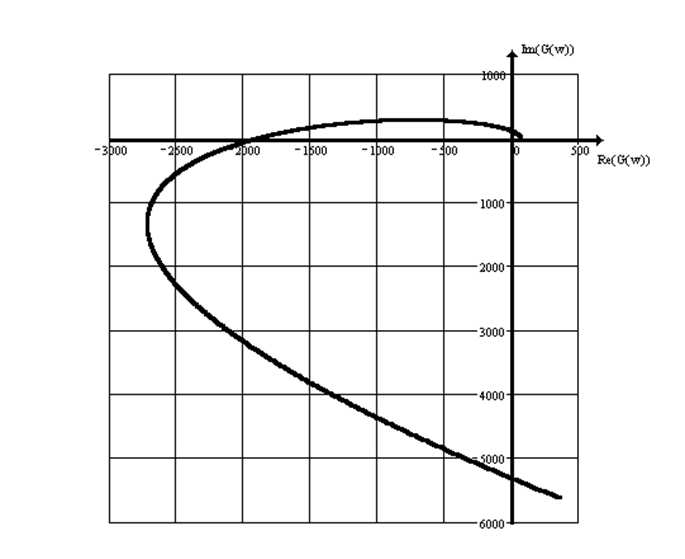
рис. 2
9. Исследовать устойчивость системы по критерию Найквиста. Построить годограф. Определить запас устойчивости по модулю и по фазе.
Исследование устойчивости системы по критерию Найквиста заключается в построении годографа функции передачи системы K(w), где p=jw, а K(w) - комплексный коэффициент передачи разомкнутой системы. K(p) найден нами в пункте 1, а коэффициенты полиномов числителя и знаменателя в пунктах 5 и 6:
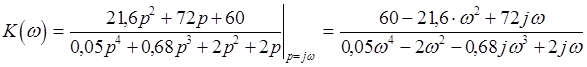, как видно из структуры выражения K(w) мы можем сделать выводы:
1) годограф начинается в точке (6 ; -j¥), под углом -90°.
2) годограф заканчивается в точке (0 ; 0), и входит в нее под углом -180°. Поведение годографа на интервале от 0 до ¥ показано на рисунке 3:
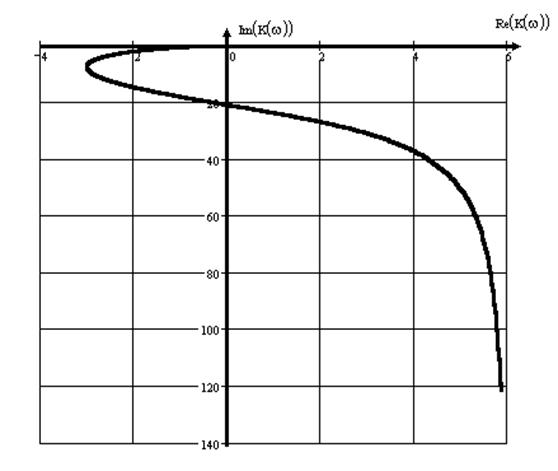
рис. 3
Так как из рисунка 3 не совсем ясно поведение годографа системы в окрестности нуля ниже приведен еще один годограф, в большем масштабе и на более высоких частотах (рисунок 4). Как видно из этого рисунка, годограф не обхватывает точку (-1;0), следовательно система устойчива. Но при изменении постоянных времени или коэффициента усиления системы возможен переход системы в состояние самовозбуждения.
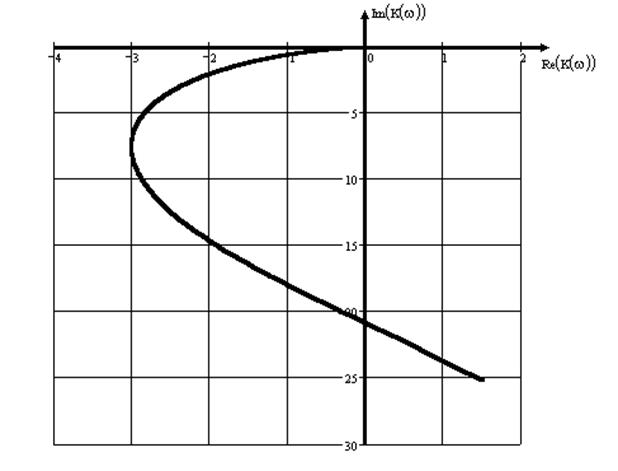
рис. 4
Определим запас устойчивости системы по модулю и по фазе. Для этого проведем на годографе Найквиста окружность еденичного радиуса. Отметим точку пересечения годографа и окружности. Запас устойчивости системы по фазе определяестся, как фаза радиус-вектора, проходящего через точку пересечения годографа с окружностью и через начало координат: Df=-152°. Так как наш годограф не пересикает вещественную ось при увелечении частоты, значит система имеет бесконечный запас устойчивости по модулю.
10. Найти x(t). Построить график.
Сигнал ошибки x(t) находиться по формуле, приведенной в [1], и равен:
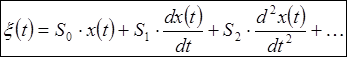(7) ,
где S0, S1, S2, …, Sn -
коэффициенты ошибки.
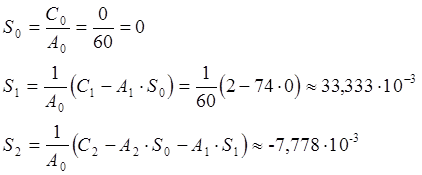
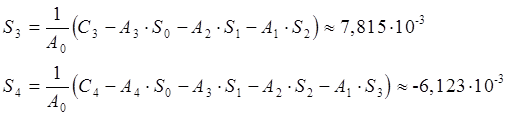
дальнейшее вычисление коэффициентов Si затруднительно и не имеет большой необходимости, так как на сигнал ошибки влияют в основном первые два члена. Подставив вычисленные коэффициенты ошибки Si в (7), и вычислив первые четыре производные сигнала, мы получим выражение для сигнала ошибки:
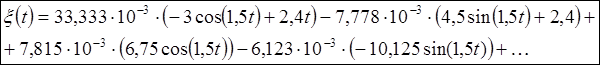(8)
Построим график, согласно выражению (8):
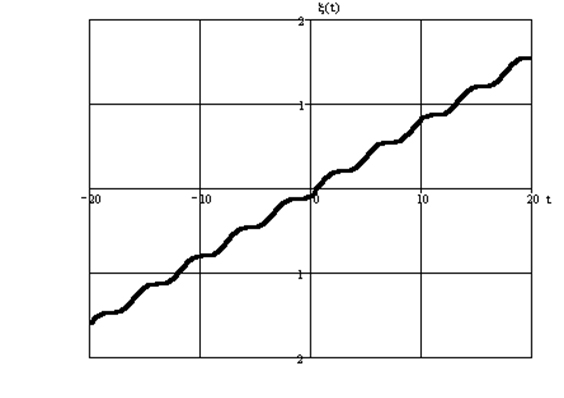
рис. 4
Список литературы:
1. Радиоавтоматика. Методические указания. С. Е. Лявданский. НГТУ. 1995 г.
2. Радиоавтоматика. Методические указания к самостоятельной лабораторной работе. С. Е. Лявданкий. НЭТИ. 1990 г.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.