Передаточная функция и дифференциальное уравнение замкнутой системы. Передаточная функция для ошибки от возмущающего воздействия

Министерство образования Российской Федерации

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра РП и РПУ

Расчетно - графическое задание по дисциплине:

“Теория управления и радиоавтоматика”.

Вариант №9.

ВЫПОЛНИЛ:                                          ПРОВЕРИЛ:

Студент группы РТ5-73                         Преподаватель: Лявданский С. Е.

Сивохин С. В.                                           Оценка:          

Дата:                           Дата:

Задание:

1.  Вычислить K(p).

2.  Зарисовать структурную схему системы, считая ее следящей. Дать названия всем входящим в нее типовым и структурным звеньям.

3.  Записать передаточную функцию и дифференциальное уравнение замкнутой системы.

4.  Записать передаточную функцию для ошибки от возмущающего воздействия.

5.  Записать характеристический полином разомкнутой системы и   вычислить его коэффициенты.

6.  Записать характеристический полином замкнутой системы и вычислить его коэффициенты.

7.  Провести анализ устойчивости системы по критерию Гурвица.

8.  Исследовать устойчивость системы по критерию Михайлова. Построить годограф.

9.  Исследовать устойчивость системы по критерию Найквиста. Построить годограф. Определить запас устойчивости по модулю и по фазе.

10.  Найти x(t). Построить график.

Исходные данные:

Передаточная функция замкнутой системы:

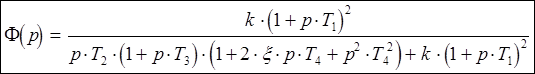(1)

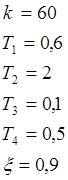
Входное воздействие:

1 .  Записать K(p).

Известно, что 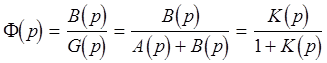, где 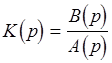- коэффициент передачи разомкнутой системы.

Путем математических преобразований получаем: 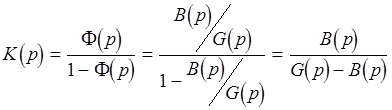, где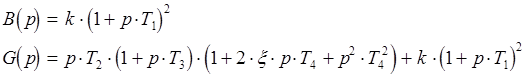

Отсюда: 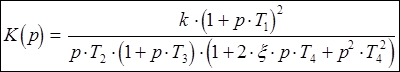(2)

2.  Зарисовать структурную схему системы, считая ее следящей. Дать названия всем входящих в систему типовых и структурных звеньев.

Составление структурной схемы производиться согласно коэффициенту передачи разомкнутой системы K(p). Ее сомножители являются коэффициентами передачи отдельных звеньев. Так, в нашем случае, система состоит из четырех звеньев. Их коэффициенты передачи:

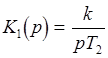 - интегрирующее звено;

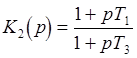 - упругое дифференцирующее звено (T₁>T₃);

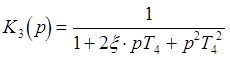 - колебательное звено;

 - форсирующее звено.

Структурная схема системы (следящей):

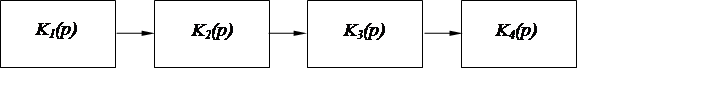
рис. 1

3. Записать передаточную функцию и дифференциальное уравнение замкнутой системы.

Передаточная функция замкнутой системы Ф(p) задана нам в исходных данных, и обозначена, как (1). Подставив в (1) численные значения коэффициентов, мы получим следующее выражение:

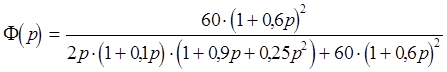
Раскроем скобки в числителе и знаменателе, и сгруппируем слагаемые по степеням р.

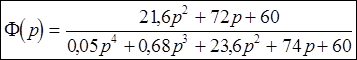(3)

Запишем дифференциальное уравнение замкнутой системы:

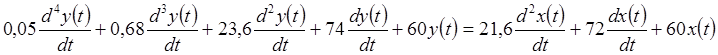
4. Записать передаточную функцию для ошибки от возмущающего воздействия.

Передаточной функцией для ошибки от возмущающего воздействия является величина 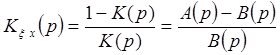. Подставив полученное в пункте 1 выражение для 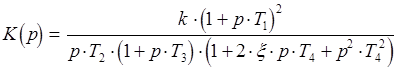 , раскрыв скобки и сгруппировав числитель и знаменатель по степеням p, мы получим, что:

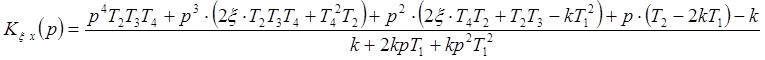Подставим в данное выражение численные значения коэффициентов:

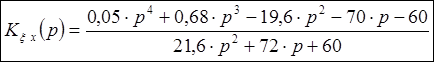 (4)

5. Записать характеристический полином разомкнутой системы и вычислить его коэффициенты.

Характеристическим полиномом разомкнутой системы является полином знаменателя передаточной функции разомкнутой системы:

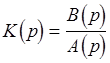, где А(р) - характеристический полином разомкнутой системы.

Подставив в (2) численные значения коэффициентов мы получим:

(5)

6. Записать характеристический полином замкнутой системы и вычислить его коэффициенты.

Характеристическим полиномом замкнутой системы является полином знаменателя коэффициента передачи 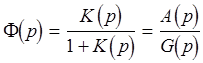, где  - характеристический полином замкнутой системы.

Подставим численные значения коэффициентов знаменателя Ф(р) в (1) получаем:

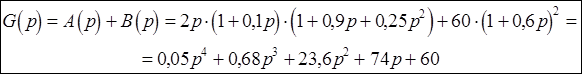(6)

7.  Произвести анализ устойчивости системы по критерию Гурвица.

Алгебраический критерий устойчивости Гурвица налагает условия на коэффициенты полинома G(p). Эти условия делятся на необходимые и достаточные.  Необходимым условием устойчивости системы является положительность всех коэффициентов полинома G(p), как видно из (6) данное условие выполняется. Проверим выполнение достаточного условия устойчивости системы.