и заданными математическим ожиданием ![]() и дисперсией
и дисперсией
![]() В2. Изобразите графики
В2. Изобразите графики ![]() и
и ![]() .
.
10. Используя результат, полученный при решении задачи 9, определите
математическое ожидание ![]() , второй начальный момент
, второй начальный момент
![]() и дисперсию
и дисперсию ![]() тока
тока ![]() .
.
11. На НЭ с характеристикой вида
(9.16) (![]() мкА,
мкА, ![]() В-1)
действует нормальный (см. формулу (9.18)) случайный процесс
В-1)
действует нормальный (см. формулу (9.18)) случайный процесс ![]() с нулевым математическим ожиданием и
дисперсией
с нулевым математическим ожиданием и
дисперсией ![]() В2. Найдите плотность вероятности
В2. Найдите плотность вероятности
![]() тока
тока ![]() .
.
12. На односторонний квадратор с характеристикой (9.13) при ![]() В-2 действует нормальный
процесс с нулевым математическим ожиданием и дисперсией
В-2 действует нормальный
процесс с нулевым математическим ожиданием и дисперсией ![]() В2.
В2.
Определите плотность вероятности ![]() и математическое ожидание
и математическое ожидание ![]() тока
тока ![]() .
.
13. Нормальный случайный процесс ![]() с нулевым математическим ожиданием и
дисперсией
с нулевым математическим ожиданием и
дисперсией ![]() В2 действует на нелинейный преобразователь с характеристикой
(9.15), при этом
В2 действует на нелинейный преобразователь с характеристикой
(9.15), при этом ![]() мА,
мА, ![]() мА/В,
мА/В, ![]() мА/ В2.
мА/ В2.
Найдите плотность вероятности ![]() тока
тока ![]() .
.
14. На затвор полевого транзистора КП103Ж, проходная характеристика (рис. 8.7) которого аппроксимирована выражением
![]() , мА,
, мА,
где ![]() мА,
мА, ![]() 1/В, подается случайный сигнал
1/В, подается случайный сигнал ![]() с равномерной плотностью вероятности
(9.14).
с равномерной плотностью вероятности
(9.14).
Определите плотность вероятности ![]() тока стока
тока стока ![]() .
.
15. Проходная характеристика полевого транзистора КП303Е описывается кусочно-нелинейной зависимостью
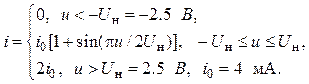
На затвор транзистора действует случайный сигнал ![]() с равномерной плотностью вероятности
(9.14).
с равномерной плотностью вероятности
(9.14).
Определите плотность вероятности ![]() тока
транзистора.
тока
транзистора.
16. Характеристика полупроводникового диода (см. рис. 8.9) аппроксимируется выражением
![]() .
.
Определите плотность вероятности ![]() и математическое
ожидание
и математическое
ожидание ![]() тока диода, если к нему приложено
случайное напряжение
тока диода, если к нему приложено
случайное напряжение ![]() с равномерной плотностью
вероятности (9.14).
с равномерной плотностью
вероятности (9.14).
17. Характеристика ![]() типового безынерционного
нелинейного устройства приведена в табл. 9.1. Входной стационарный случайный
процесс
типового безынерционного
нелинейного устройства приведена в табл. 9.1. Входной стационарный случайный
процесс ![]() характеризуется симметричным законом
распределения
характеризуется симметричным законом
распределения ![]() с нулевым математическим ожиданием:
с нулевым математическим ожиданием:
а) ![]() ;
;
б) ![]() .
.
Определите плотность вероятности ![]() процесса
процесса
![]() на выходе устройства.
на выходе устройства.
Таблица 9.1
|
№ п/п |
Тип устройства |
Аппроксимирующая функция |
|
|
Выражение |
График |
||
|
1 |
Нелинейный усилитель |
при |
|
|
2 |
Нелинейный усилитель |
|
|
|
3 |
Нелинейный усилитель |
|
|
|
4 |
Односторонний квадратичный детектор (квадратор) |
|
|
|
5 |
Двусторонний квадратичный детектор |
|
|
Окончание табл. 9.1
|
№ п/п |
Тип устройства |
Аппроксимирующая функция |
|
|
Выражение |
График |
||
|
6 |
Односторонний Ограничитель |
|
|
|
7 |
Двусторонний ограничитель |
|
|
|
8 |
Компаратор (пороговое устройство) |
|
|
|
9 |
Квантователь на два уровня |
|
|
|
10 |
Квантователь на три уровня |
|
|
9.4. Контрольное задание
Воздействие стационарного случайного сигнала на безынерционный нелинейный элемент
На вход нелинейного безынерционного элемента действует стационарный
случайный процесс ![]() с одномерной плотностью
вероятности
с одномерной плотностью
вероятности ![]() . Характеристика нелинейного элемента, вид
аппроксимирующей функции и смещение такие же, что и в задании 8.
Среднеквадратическое значение напряжения
. Характеристика нелинейного элемента, вид
аппроксимирующей функции и смещение такие же, что и в задании 8.
Среднеквадратическое значение напряжения ![]() случайного
процесса взять равным
случайного
процесса взять равным ![]() из задания 8 (табл.8.3).
из задания 8 (табл.8.3).
Закон распределения вероятностей входного случайного процесса:
· равномерный – для вариантов 0–7
![]() при
при ![]() ,
,
где ![]() ;
;
· нормальный (гауссов) – для вариантов 8–9
![]() .
.
Требуется:
а) определить одномерную плотность вероятности ![]() на выходе НЭ;
на выходе НЭ;
б) построить графики ![]() и
и ![]() ;
;
в) найти математическое ожидание ![]() , дисперсию
, дисперсию
![]() и среднюю мощность
и среднюю мощность ![]() случайного
процесса на выходе безынерционного НЭ.
случайного
процесса на выходе безынерционного НЭ.
Методические указания
Вопросы преобразования случайных процессов в безынерционных нелинейных цепях даны в [1¼3], а примеры и задачи – в [7¼9].
При нахождении одномерной плотности вероятности ![]() для НЭ, аппроксимированного
кусочно-линейной зависимостью, проверьте условие нормировки
для НЭ, аппроксимированного
кусочно-линейной зависимостью, проверьте условие нормировки
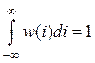 .
.
Для выполнения этого условия ввести при необходимости в выражение ![]() слагаемое в виде дельта-функции (Дирака)
слагаемое в виде дельта-функции (Дирака) ![]() с соответствующим коэффициентом
с соответствующим коэффициентом ![]() , т. е.
, т. е. ![]() .
.
Для вариантов 8 и 9 следует воспользоваться справочными данными, приведенными в прил. П.3 и П.7.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.