В частности, при ![]() (линия 2 на
рис. 9.3, а), пороги
(линия 2 на
рис. 9.3, а), пороги ![]() и
и ![]() “сливаются” в один
“сливаются” в один ![]() ,
а выходной процесс
,
а выходной процесс ![]() может принимать только одно из
двух квантованных значений 0 (логический “0”) или
может принимать только одно из
двух квантованных значений 0 (логический “0”) или ![]() (логическую
“1”) соответственно с вероятностью
(логическую
“1”) соответственно с вероятностью ![]() и
и ![]() (рис. 9.3, в). В этом заключается
принцип функционирования порогового устройства, а также квантователя на два
уровня
(рис. 9.3, в). В этом заключается
принцип функционирования порогового устройства, а также квантователя на два
уровня
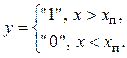 (9.7)
(9.7)
Аналогичным образом можно обобщить рассмотрение на случай ограничения
и квантования с ![]() уровнями.
уровнями.
Моменты распределения
Наиболее важными для практического использования являются моменты
первых двух порядков: математическое ожидание ![]() ,
среднее значение квадрата
,
среднее значение квадрата ![]() и дисперсия
и дисперсия ![]() ; при этом они могут быть вычислены двумя
эквивалентными способами:
; при этом они могут быть вычислены двумя
эквивалентными способами:
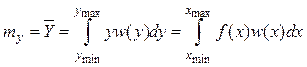 ,
(9.8)
,
(9.8)
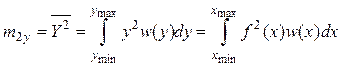 , (9.9)
, (9.9)
![]() .
(9.10)
.
(9.10)
Смешанные начальный и центральный моменты второго порядка, характеризующие взаимосвязь мгновенных значений в двух произвольных сечениях (быстродействие процесса) и называемые соответственно автоковариационной и автокорреляционной функциями, описываются выражениями:
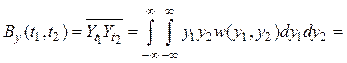
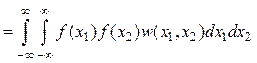 .
(9.11)
.
(9.11)
![]() ,
(9.12)
,
(9.12)
здесь ![]() и
и ![]() –
двумерная плотность вероятности процессов
–
двумерная плотность вероятности процессов ![]() и
и ![]() ,
, ![]() – якобиан
преобразования переменных [2, 3].
– якобиан
преобразования переменных [2, 3].
Примечание. Определение названных функций по формулам (9.11) и (9.12) представляет собой довольно сложную задачу ввиду трудности вычисления интегралов, содержащих двумерные плотности. В случае линейных цепей задача существенно упрощается, так как по корреляционной функции входного процесса (а ее для эргодических процессов можно определить, минуя использование двумерной плотности) легко определить спектральную плотность мощности (СПМ), а затем согласно принципу суперпозиции – выходную СПМ и автокорреляционную функцию. Для нелинейных цепей принцип суперпозиции не применим, и невозможно избежать использования двумерной плотности даже для эргодических процессов.
9.3. Задачи
1. Характеристика нелинейного элемента аппроксимирована квадратичной параболой и прямой (задача 8.2):
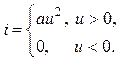 (9.13)
(9.13)
На вход НЭ подан стационарный случайный процесс – напряжение ![]() с плотностью вероятности:
с плотностью вероятности:
![]() .
(9.14)
.
(9.14)
Определите и изобразите плотность вероятности ![]() тока НЭ. Изобразите (качественно) функцию
распределения
тока НЭ. Изобразите (качественно) функцию
распределения ![]() .
.
2. Решите задачу 1 для случая, когда ![]() мА/В2,
мА/В2,
![]() В,
В, ![]() В.
В.
3 Проанализируйте результат решения задачи 1: а) при уменьшении
смещения ![]() ; при этом изобразите графики
; при этом изобразите графики ![]() для случаев: 1)
для случаев: 1) ![]() ,
2)
,
2) ![]() ; б) при увеличении величины b (и неизменном исходном значении
; б) при увеличении величины b (и неизменном исходном значении ![]() ),
включая случай, когда
),
включая случай, когда ![]() .
.
4. По условию задач 1 и 2 определите основные моменты распределения
тока НЭ: математическое ожидание ![]() , второй началь-
, второй началь-
ный момент ![]() ,
дисперсию
,
дисперсию ![]() . Решение проведите сначала в общем виде, а
затем – с подстановкой численных значений. Найдите также мощность постоянной
составляющей
. Решение проведите сначала в общем виде, а
затем – с подстановкой численных значений. Найдите также мощность постоянной
составляющей ![]() , мощность флюктуаций
, мощность флюктуаций ![]() и полную среднюю мощность
и полную среднюю мощность ![]() на сопротивлении нагрузки
на сопротивлении нагрузки ![]() кОм.
кОм.
5. Найдите одномерную плотность вероятности ![]() случайного
процесса
случайного
процесса ![]() , получаемого на выходе НЭ с характеристикой
(см. рис. 8.1) (мА)
, получаемого на выходе НЭ с характеристикой
(см. рис. 8.1) (мА)
![]() ,
(9.15)
,
(9.15)
где ![]() мА,
мА, ![]() мА/В,
мА/В, ![]() мА/В2, при воздействии на его
вход стационарного случайного процесса
мА/В2, при воздействии на его
вход стационарного случайного процесса ![]() с плотностью
вероятности вида (9.14) с
с плотностью
вероятности вида (9.14) с ![]() В,
В, ![]() В.
В.
6. По данным задачи 5 найдите математическое ожидание ![]() , второй начальный момент
, второй начальный момент ![]() и дисперсию
и дисперсию ![]() тока
тока ![]() .
.
7. На двусторонний квадратор с характеристикой ![]() (например, на схему с двухтактным
включением диодов) действует процесс
(например, на схему с двухтактным
включением диодов) действует процесс ![]() с плотностью
вероятности
с плотностью
вероятности ![]() (9.14); при этом
(9.14); при этом ![]() .
.
Определите плотность вероятности ![]() тока
тока ![]() ; изобразите график
; изобразите график ![]() .
.
8. Характеристика НЭ аппроксимирована экспонентой
![]() ,
(9.16)
,
(9.16)
где ![]() мкА,
мкА, ![]() В-1
(задача 8.6). На НЭ воздействует случайный
процесс
В-1
(задача 8.6). На НЭ воздействует случайный
процесс ![]() с плотностью вероятности (9.14) с
с плотностью вероятности (9.14) с ![]() В и
В и ![]() В. Найдите плотность вероятности
В. Найдите плотность вероятности ![]() и изобразите график. Проанализируйте
влияние изменения параметров сигнала (
и изобразите график. Проанализируйте
влияние изменения параметров сигнала (![]() и
и ![]() ) и характеристики НЭ (
) и характеристики НЭ (![]() и
и ![]() ) на
форму графика.
) на
форму графика.
9. Определите плотность вероятности тока на выходе НЭ, характеристика которого аппроксимирована кусочно-линейной зависимостью
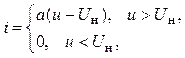 (9.17)
(9.17)
где ![]() В,
В, ![]() мА/В.
На вход НЭ подается нормальный случайный процесс
мА/В.
На вход НЭ подается нормальный случайный процесс ![]() с
плотностью вероятности
с
плотностью вероятности
![]() ,
(9.18)
,
(9.18)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.