На промежутке T1 < t < (T1+ T2) реализация СП изменяется линейно от значения -Um до 0, поэтому на промежутке -Um < u < 0 функция распределения вероятности меняется тоже линейно от значения F(-Um) до 1. Таким образом, математическое описание функции распределения имеет вид:
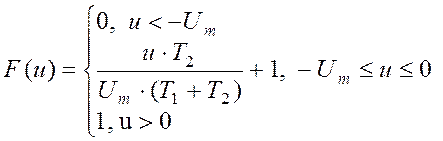
Функцию
плотности распределения вероятности w(u) можно определить как
производную от функции распределения F(u):
На интервалах u < -Um , u > 0 функция распределения постоянна, поэтому w(u) = 0 на этих участках.
В промежутке -Um < u ≤ 0 изменеие F(u) имеет линейный характер, следовательно
w(u)
= const =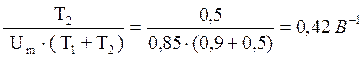
При значении, которое в определённый промежуток времени является постоянным для реализации СП, т.е. при u = -Um функция плотности распределения равна дельта-функции: w(u) = k · δ(u + Um), где k = P(-Um) = T1/( T1+ T2) = 0,9 / (0,9 + 0,5) = 0,643.
Окончательно, выражение для плотности
распределения вероятности имеет вид:
w(u) =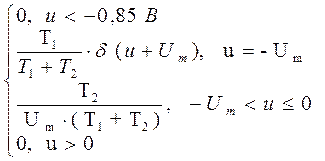 
Найдём математическое ожидание методом усреднения по множеству реализаций, учитывая условие нормировки для δ-функции:
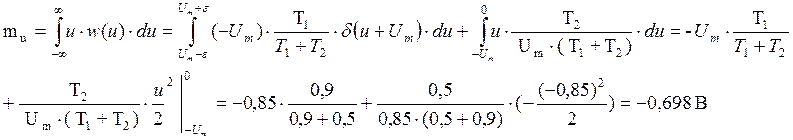
Найдём mu методом усреднения по времени одной реализации:
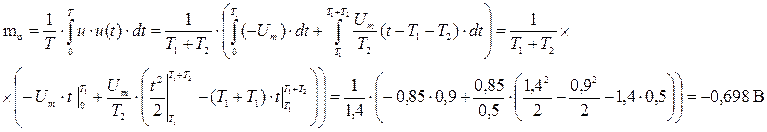
Вычислим дисперсию методом усреднения по множеству реализаций:
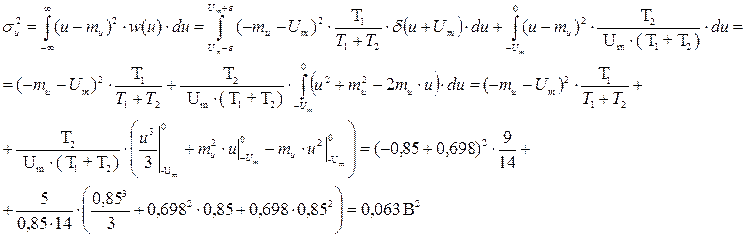
Найдём дисперсию методом усреднения по времени одной реализации:
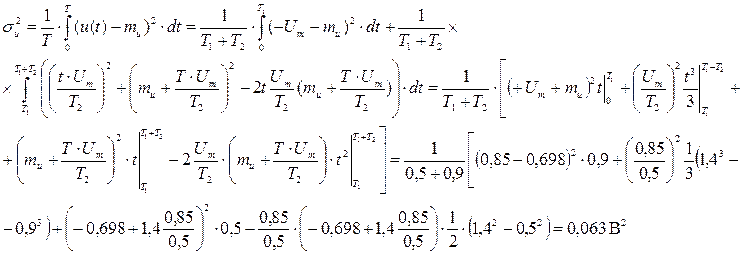
Исходя из значения дисперсии, найдём среднеквадратическое отклонение: 
Вычислим вероятность нахождения значения случайного процесса в интервале от U1 до U2:
 |
|||
 |
|||
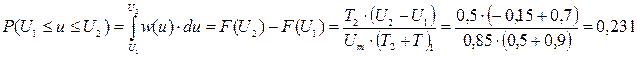
Определение корреляционной функции сигнала через его энергетический спектр.
Требуется: для случайного сигнала с заданным энергетическим спектром W(w), вид которого представлен на рис. 6, определить:
а) корреляционную функцию K(t);
б) эффективную ширину спектра;
в) интервал корреляции.
Функция корреляции и энергетический спектр связаны между собой теоремой Хинчина-Винера:
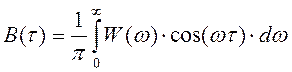
Подставив в это выражение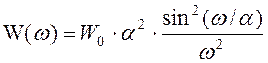 
,
получим:
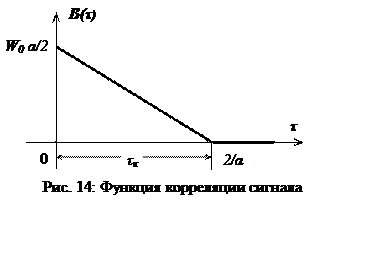
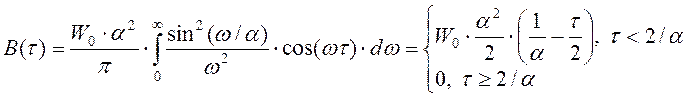
Найдём эффективную ширину спектра сигнала, т.е. полосу частот, в которой содержится основная часть энергии сигнала:
∆ωэфф =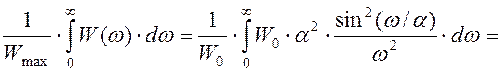 
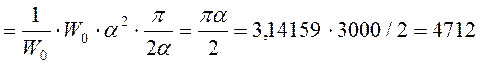рад/с
Вычислим интервал корреляции, т.е. временной интервал, на краях которого статистическая связь между значениями СП становится незначительной:
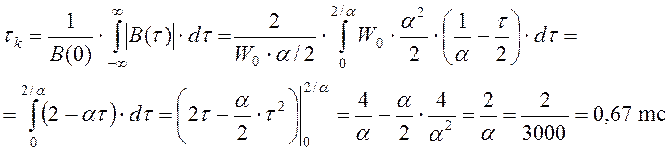
Проверим полученные результаты, используя соотношение неопределённости между эффективной шириной спектра и интервалом корреляции:
∆ωэфф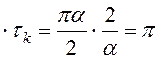
, т.е.
соотношение выполняется.
Нелинейное преобразование сигналов.
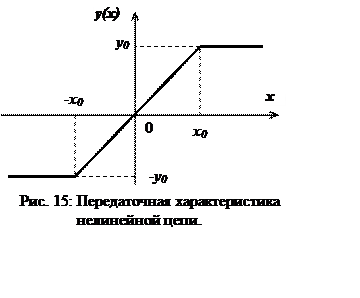Задание: определить
плотность распределения вероятностей процесса на выходе цепи через заданную плотность
распределения процесса на входе и передаточную характеристику цепи, а также
математическое ожидание, дисперсию и среднеквадратическое отклонение сигнала на
выходе цепи.
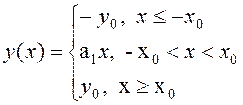
Плотность распределения вероятности процесса на выходе нелинейной безынерционной цепи связан с плотностью распределения процесса на входе следующим выражением:
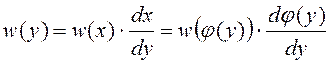
Так как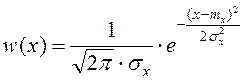 
и 
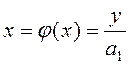, то
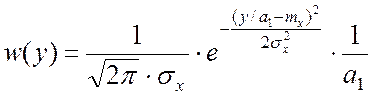, на участке 
Передаточная функция цепи ограничивает значения
выходного сигнала интервалом 
, поэтому при значених у, выходящих за пределы этого
промежутка, функция плотности распределения вероятности процесса y(t)
равна нулю.
На границах этого интервала, т.е. при значениях y = -y0 и у = y0 функция 
равна δ-функции.
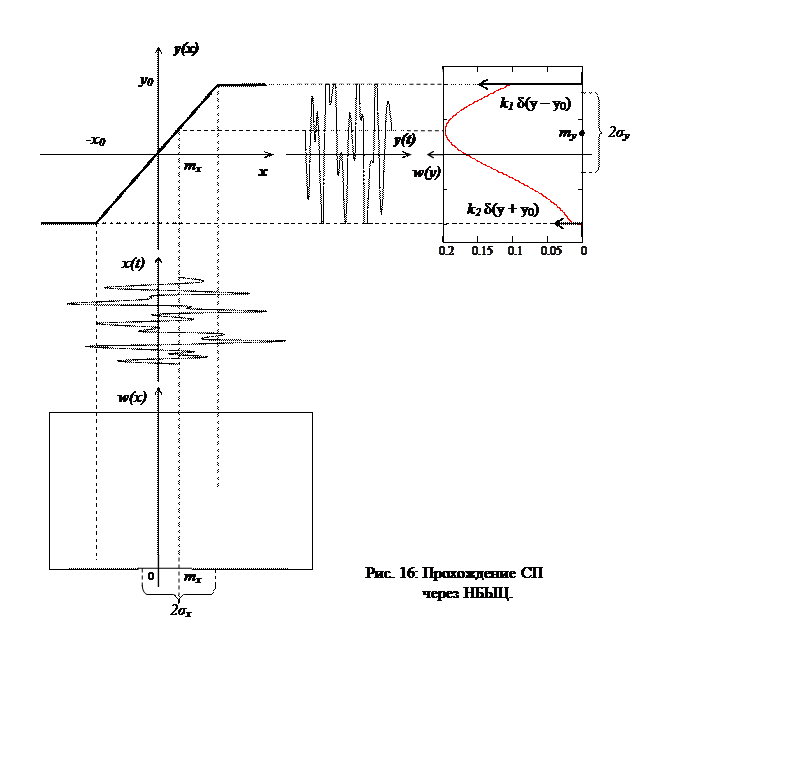
Таким образом, полное математическое описание функции плотности распределения вероятности процесса на выходе НБЫЦ, изображённой на рис. 16, имеет вид:
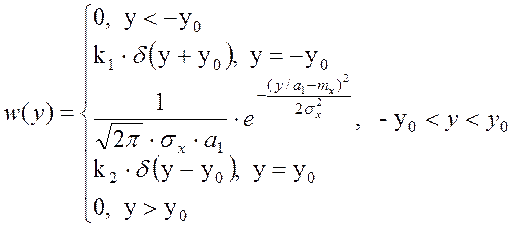
Найдём коэффициенты 
и 
, учитывая,
что площадь под кривой функции плотности распределения всегда равна единице:
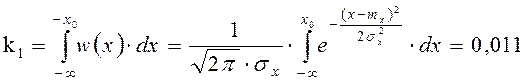
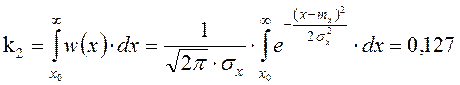
Найдём числовые характеристики сигнала на выходе цепи:
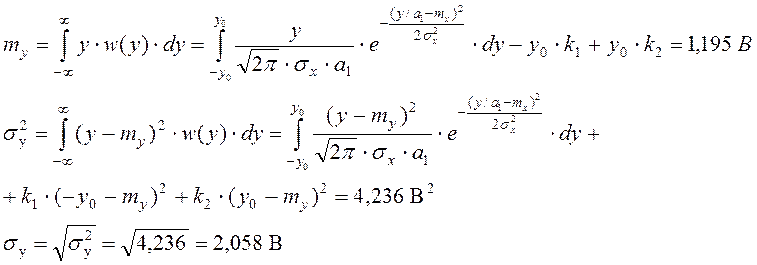
Заключение
Курсовая работа способствует закреплению навыков и формированию умений по математическому описанию сигналов, определению их вероятностных и числовых характеристик. Ведь статистическое описание радиотехнических сигналов, оценивание их физических характеристик является математическим "инструментом" радиоинженера при решении многообразных практических задач.
В данной работе был произведён ряд вычислений, наиболее полно отражающий содержание курса. В частности были найдены числовые характеристики (математическое ожидание, дисперсия и среднеквадратическое отклонение двумя различными способами: методом усреднения по множеству реализаций и методом усреднения по времени одной длинной реализации, давшими одинаковый результат), функция распределения вероятности и функция плотности распределения вероятности эргодического случайного процесса, найдена корреляционная функция случайного процесса через его энергетический спектр а также интервал корреляции и эффективная ширина спектра сигнала, удовлетворяющие известному соотношению, кроме того, определена плотность распределения вероятности на выходе нелинейной цепи по известной плотности распределения на входе, а также составлена структурная схема радиотехнической системы передачи непрерывных сообщений дискретными сигналами.
Список использованной литературы
1. Гоноровский И. С. Радиотехнические цепи и сигналы: Учебник для вузов. – 4-е изд., перераб. и доп. – М.: Радио и связь, 1986. – 512 с.
2. Гоноровский И. С., Дёмин М. П. Радиотехнические цепи и сигналы: Учеб. Пособие для вузов. – 5-е изд., перераб. и доп. – М.: Радио и связь, 1994. – 480 с.
3. Баскаков С. И. Радиотехнические цепи и сигналы: Учебник для вузов по спец. «Радиотехника». – 4-е изд., перераб. и доп. – М.: Высшая школа, 2003. – 452 с.
4. Баскаков С. И. Радиотехнические цепи и сигналы: Руководство к решению задач: Учеб. пособие для для радиотехн. спец. вузов. – М.: Высшая школа, 1987. – 207 с.
5. Радиотехнические цепи и сигналы. Примеры и задачи: Учеб. пособие для вузов. / Г. Г. Галустов, И. С. Гоноровский, М. П. Дёмин и др.; Под ред. И. С. Гоноровского. - М.: Радио и связь, 1989.
6. Чернецкий Г. А. Радиотехнические цепи и сигналы: Методические указания к курсовой работе. – Новосибирск: СибГУТИ, 1999. – 24 с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.