Разработка обобщенной структурной схемы радиотехнической системы связи для передачи непрерывных сообщений дискретными сигналами, страница 3

Задан энергетический спектр сигнала:

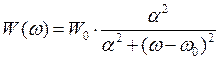
Где ,

.

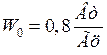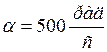
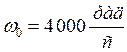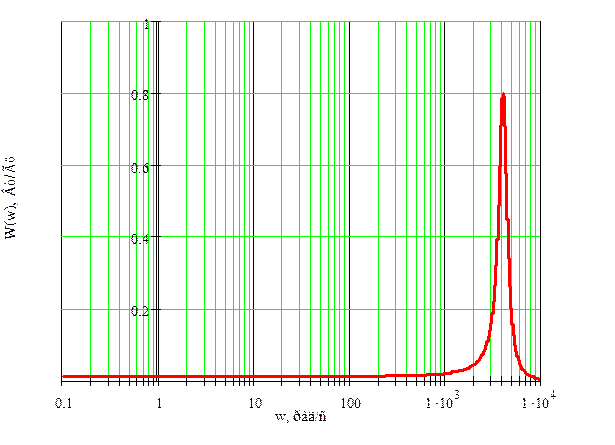
Рисунок 16 – Функция энергетического спектра

Корреляционный анализ делается на основе теоремы Винера – Хинчина, устанавливающий связь между энергетическим спектром случайного сигнала и его ковариационной функцией с помощью парой преобразовании Фурье.

Для упрощения расчетов учитываем особенность определения функции корреляции узкополосного случайного процесса, для этого в выражении Винера – Хинчина сделаем замену переменной ω на переменную ,

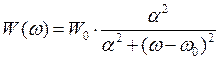 на 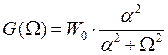. Тогда интегрирование   производим по переменной Ω на интервале от 0 до +∞.

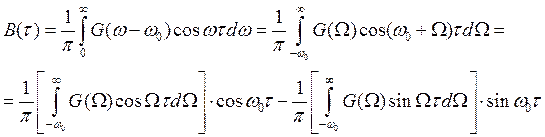
Учитывая, что в  по заданию (4 000>> 500, на порядок больше), функция корреляции узкополосного случайного процесса будет определяться выражением:

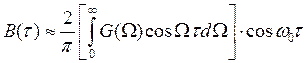
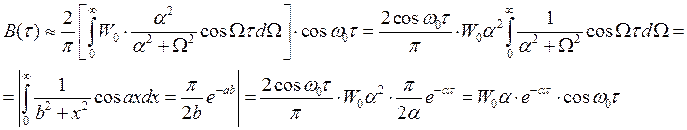
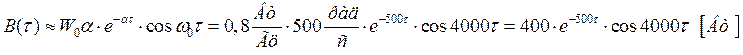
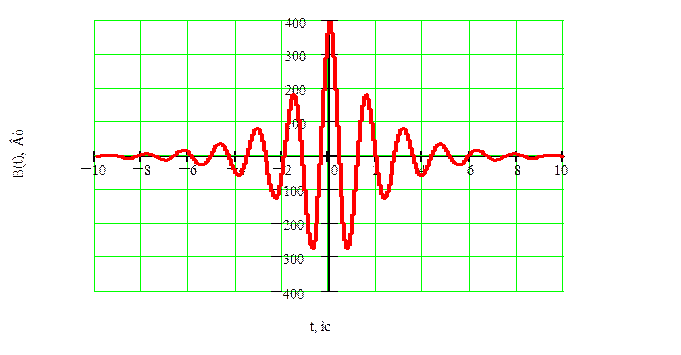
Рисунок 17 – Корреляционная функция

Эффективная ширина спектра:

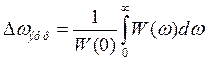
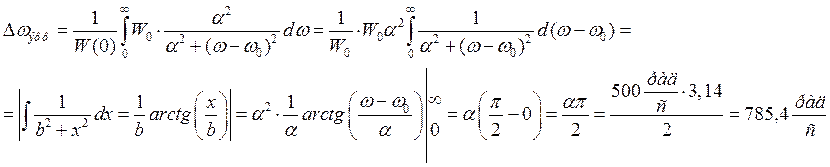
Итак, =785,4  или =125 Гц

Интервал корреляции находится, учитывая связь между эффективной шириной спектра:

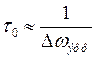
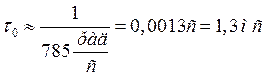
5.Нелинейное преобразование сигналов

По сравнению с линейными цепями, которые неспособны обогатить спектральный состав колебаний, поданных на ее вход, нелинейные цепи обладают гораздо большими возможностями в этом отношении, в которых связь между входным сигналом  и выходной реакцией  устанавливается нелинейная функциональная зависимость . Заданная цепь безынерционная, значит, на значение сигнала на выходе не влияет значения сигнала на входе в предыдущие моменты времени, а только именно в этот момент времени.

Дан стационарный гауссовский случайный процесс u(t) с параметрами  и .

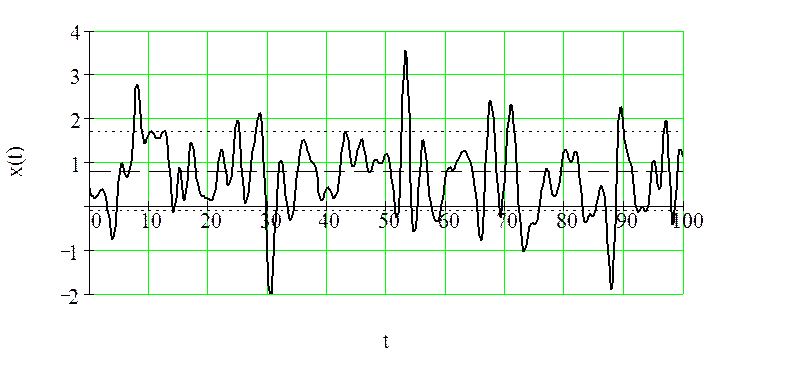Рисунок 18 – Случайный процесс

Воздействует на безынерционную цепь с характеристикой y(x).

 или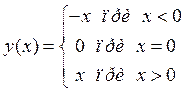

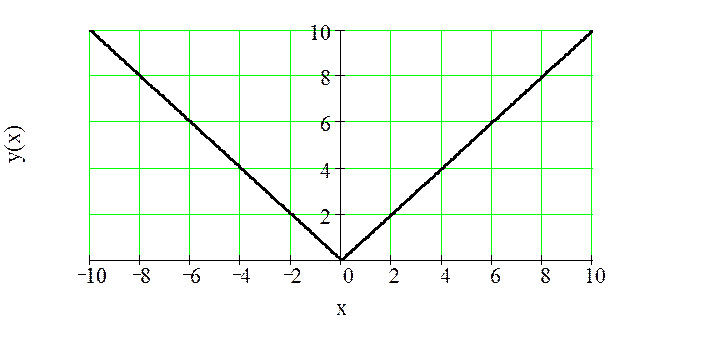
Рисунок 19 – Характеристика безынерционного нелинейного устройства

Так как процесс на входе нелинейной безынерционной цепи является гауссовским, то его одномерная плотность распределения вероятности мгновенных значении будет вида:

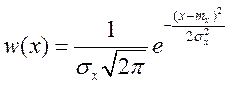
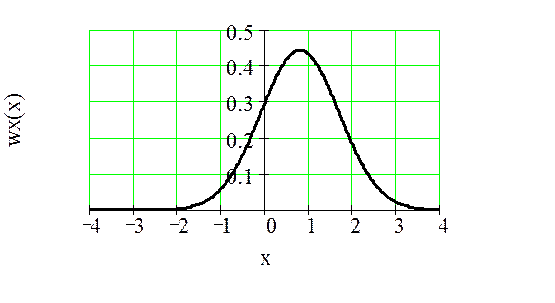
Рисунок 20 – Плотность вероятности случайного процесса с заданными числовыми характеристиками

Процесс на выходе цепи определяется проекцией сигнала на входе на характеристику НБЫЦ (см. Рисунок 24):

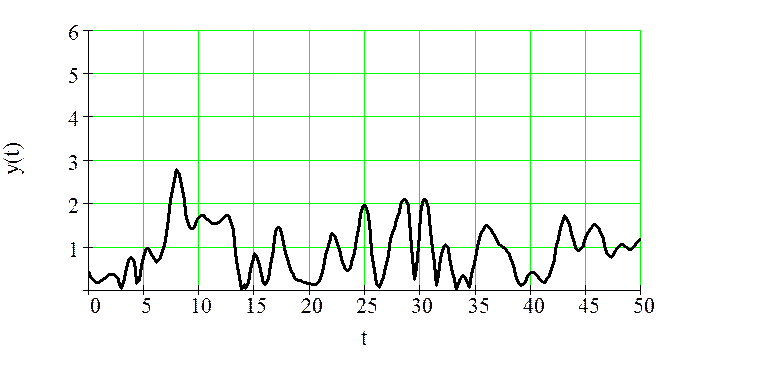Рисунок 21 – Процесс на выходе БЫЦ

Плотность распределения мгновенных значений процесса на выходе устройства  представляется через известное распределение входного процесса  на основе соотношения для функционально связанных случайных величин:

,

Где D – якобиан преобразования от переменной x  к переменной y, который для одномерной функций y=f(x) имеет вид:

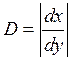
Тогда 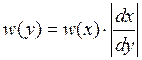 или с учетом обратной функции :

.

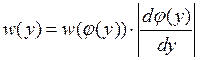Если выразить x через y, то получиться: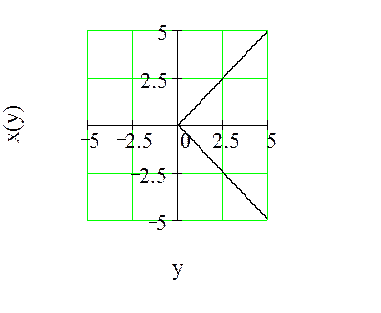

Рисунок 22 – Обратная функция  

Как видно, функция  неоднозначна, тогда:

,

Где  - значения входной величины x, соответствующей рассматриваемому значению y.

 можно представить так:

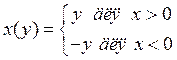, тогда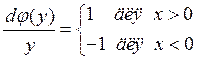

 имеет вид:

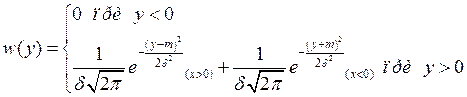
Рисунок 23 – Плотность вероятности сигнала на выходе НБЫЦ

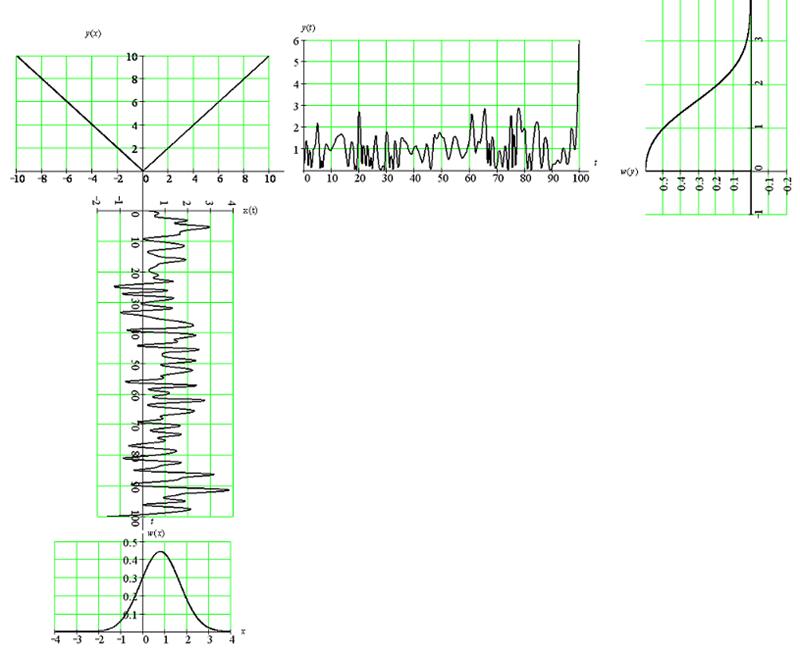
Рисунок 24 – Процесс нахождения плотнос                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                         ти распределения вероятности  процесса на выходе цепи

Определим числовые характерисктики сигнала на выходе НБЫЦ:

Мат.ожидание:

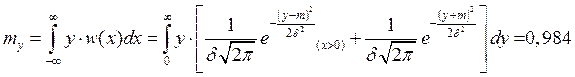
Дисперсия:

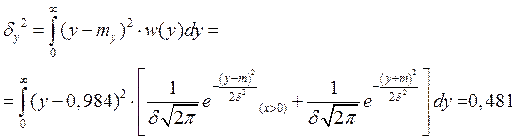
Среднеквадратическое отклонение:

Покажем на графике:

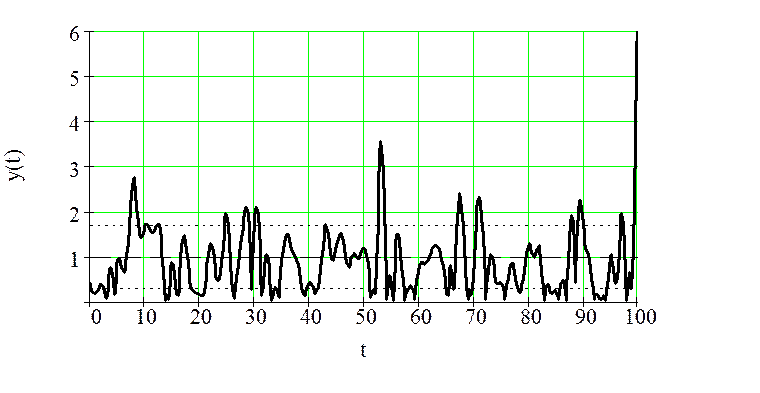Рисунок 25 – Сигнал на выходе НБЫЦ с показанными мат.ожиданием и среднеквадратическим отклонением

Заключение

Курс радиотехнические цепи и сигналы посвящен основам радиотехники и является фундаментальной радиотехнической дисциплиной. Теоретическая радиотехника насыщена понятиями и методами из разных научных областей, прежде всего математики, физики, теории цепей. В этом семестре нам понадобилась теория вероятности, как инструмент, выводящий на бумагу всю физику процессов.

Все понятия и методы, использованные в данной курсовой работе, образуют взаимосвязанное единство по анализу и синтезу любых радиотехнических цепей.

Список использованной литературы

1.  Конспект лекции

2.  Баскаков С.И., Радиотехнические цепи и сигналы: Учеб. для вузов. – М.: Высшая школа, 2003. – 462 с.

3.  Бакалов В.П., Дмитриков В.Ф., Крук Б.Е., Основы теории цепей: Учеб. для вузов. – М.:Радио и связь, 2000. – 592 с.