Разработка обобщенной структурной схемы радиотехнической системы связи для передачи непрерывных сообщений дискретными сигналами, страница 2

Дискретизатор, ГОИ, Квантователь и модулятор образуют аналого-цифровой преобразователь (АЦП). На выходе АЦП получаем чисто цифровой сигнал, т.е. последовательность 1 и 0.

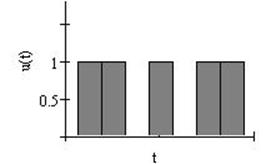
Рисунок 7 – Цифровая последовательность на выходе АЦП

Кодер статический проверяет информацию на избыточность. Если информация избыточная, сжимает эту информацию. (Например, архиваторы WinRAR, ZIP).

Кодер помехоустойчивый (ПУ) наоборот дает информации избыточность, так чтоб на приеме можно было полностью восстановить сигнал даже если в канале связи были провалы.

Устройство преобразования сигнала (модулятор) перемещает сигнал в высокочастотную область спектра для передачи. Выбираю амплитудную модуляцию, как самое простое и доступное.

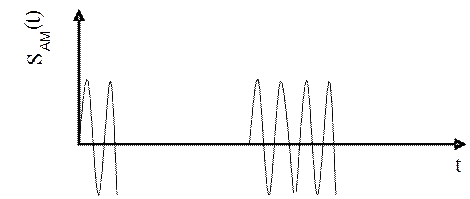
Рисунок  8 – Модулированный сигнал

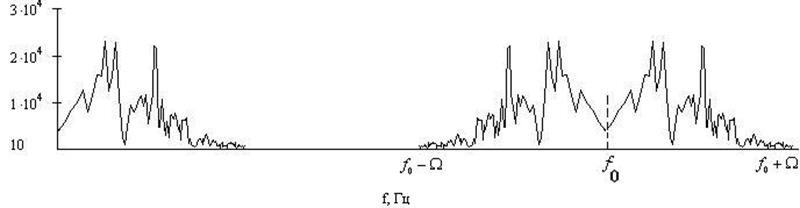
Рисунок 9 –Амплитудный спектр модулированного сигнала

Все вышеперечисленное является передающей частью РТС. Дальше сигнал попадает в канал связи, где неизбежно к нему суммируются помехи.

Рисунок 10 – Цифровой сигнал с помехами z(t)

Сигнал с помехами попадает в УПС приема. Происходит демодуляция сигнала вместе с помехами, на выходе УПС остается только низкочастотная составляющая сигнала, т.е. его полезная часть (см. рисунок 7).

Декодер ПУ восстанавливает сигнал полностью, делает обратную операцию кодер ПУ.

Декодер статический восстанавливает изначальную избыточность сигнала.

Далее сигнал попадает в цифро-аналоговый преобразователь (ЦАП), с такой же разрядностью, как и у АЦП, где происходит обратное преобразование- восстановление аналогового сигнала из принятых импульсов – кодовых комбинаций. В состав ЦАП входит детектирующее устройство, предназначенное для преобразования кодовых комбинаций в квантованную последовательность отсчетов и сглаживающий фильтр, восстанавливающий непрерывное сообщение по квантованным значениям. Сигнал на выходе ЦАП имеет вид как на рисунке 2.

Сигнал поступает к получателю сообщении.

 
3.Вероятностные и числовые характеристики

Заданная реализация эргодического сигнала u(t):

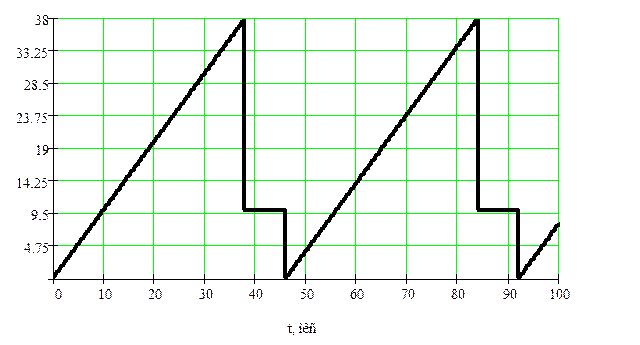
Рисунок 11 – Реализация сигнала

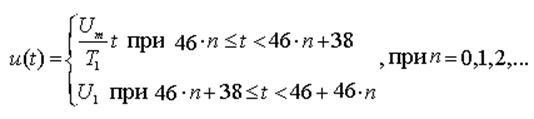
3.1.Определение вероятностных характеристик

В реальности сигналы не являются детерминированными, т.е. его мгновенные значения заранее не предсказуемы. Но всегда присутствуют вероятностные законы. Эти законы в РТЦС выражаются через плотность распределения вероятности мгновенных значений сигнала и функцией распределения вероятности.

Одномерная плотность распределения вероятности мгновенных значений по заданной реализации сигнала  эргодического сигнала показывает вероятность нахождения значения сигнала на определенном промежутке  и определяется соотношением:

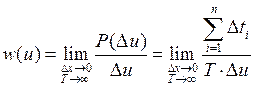
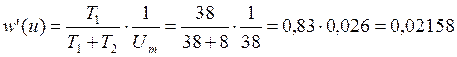
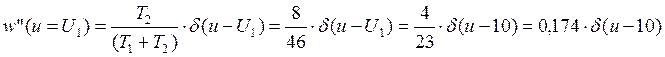
По условию нормировки должно быть 1.

Проверим это:

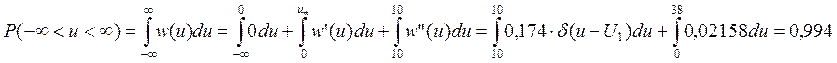
Условие нормировки выполняется. Представим плотность распределения вероятности мгновенных значений  графически:

Рисунок 12 – Одномерная плотность распределения вероятностей мгновенных значений

Функция распределения вероятности F(u) показывает вероятность сигнал примет значение, меньшее или равное конкретного значения U b определяется как:

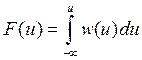
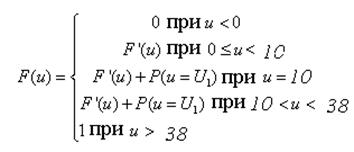
Где   

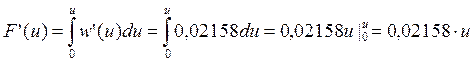
Таким образом,

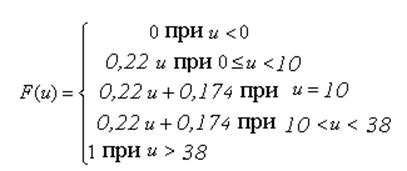
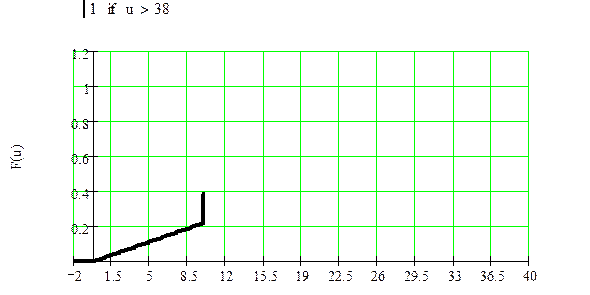
Рисунок 13 – Функция распределения вероятности

3.2. Определение числовых характеристик

Все используемые математические методы нужны для описания физической стороны процесса. Нам нужно найти мат. ожидание, значит ищем постоянную составляющую напряжения или тока, дисперсия показывает мощность переменной составляющей.

Известно свойство эргодического сигнала, позволяющее, перейти от множества испытаний к одному испытанию и, при этом, полученные характеристики распространяются на все множество. Числовые характеристики, найденные усреднением по одной, достаточно длинной реализации, равны с вероятностью 1 найденным усреднением по множеству. Проверим это свойство эргодического сигнала, заодно найдем числовые характеристики процесса (математическое ожидание, дисперсия и среднеквадратическое отклонение).Итак,

- методом усреднением по времени:

Математическое ожидание:

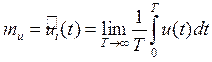
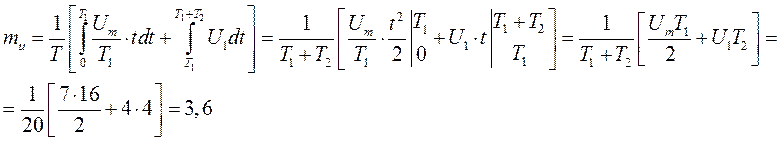
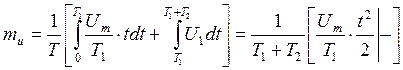
Дисперсия:

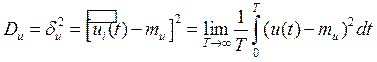
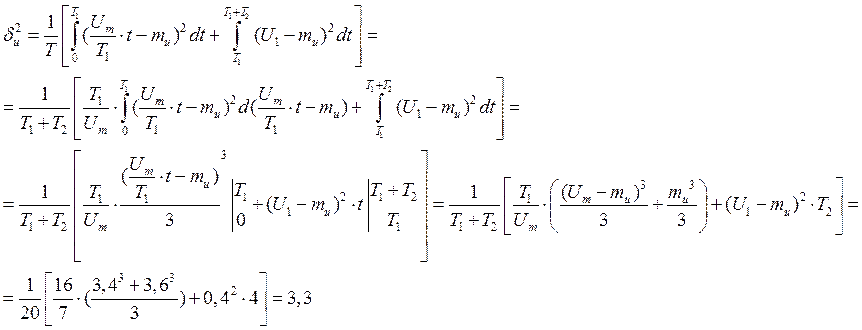
Среднеквадратическое отклонение:

- методом усреднения по множеству реализации.

Математическое ожидание:

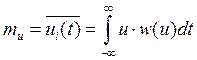
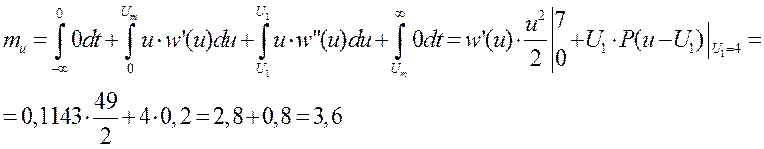
Дисперсия:

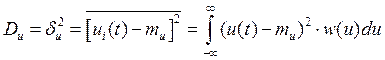
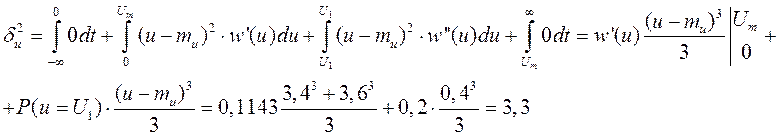
Среднеквадратическое отклонение:

Покажем числовые характеристики на графике:

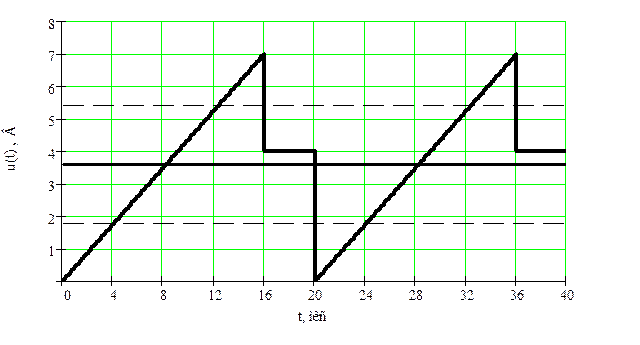
Рисунок 14 – Сигнал  с указанными числовыми характеристиками

3.3.

Вероятность того, что значение сигнала превысят заданный уровень анализа , т.е.

, где =5В.

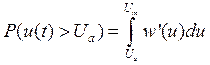
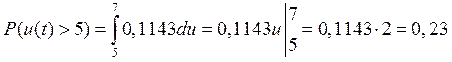
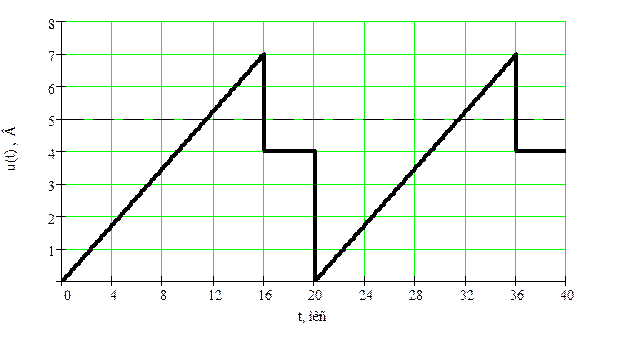
Рисунок 15 – К определению вероятности, что u(t) > 5В
4. Определение корреляционной функций сигнала

Наряду с полным описанием свойств случайных сигналов с помощью числовых и вероятностных характеристик существует другой подход, когда процессы характеризируются своими моментальными функциями. Это корреляционная теория. На основе законов этой теории, найдем корреляционную функцию заданного сигнала.