Получение АМ колебания, коэффициента модуляции

Задание 10.1    Дано: нелинейный резонансный усилитель. На вход схемы подается напряжение: . В качестве нагрузки включен резонансный контур с . Параметры:

; ; ; ; ; ; ;

1. Построить ВАХ НЭ.

2. Рассчитать и построить колебательную характеристику.

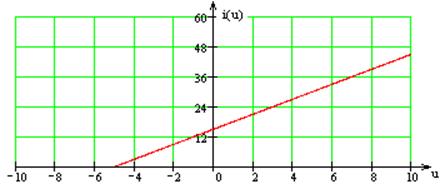
Применим для нахождения этой зависимости метод Берга. Амплитуда первой гармоники вычисляется по формуле:

Вычислим угол отсечки *

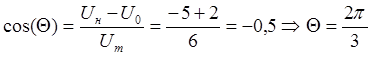
Таким образом зависимость - линейная.

3. Рассчитать и построить спектр тока НЭ.

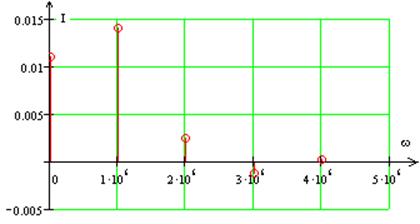
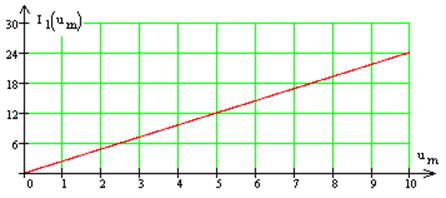
Амплитуды тока определяются по формуле:

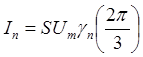
Таким образом получаем:

4. Определение амплитуды рабочей гармоники

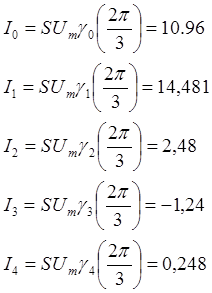
Определим резонансное сопротивление контура:

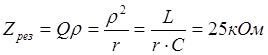
(Емкость контура находится из условия резонанса)

Таким образом, напряжение на выходе НЭ:

= 8.146 В

Напряжение на колебательном контуре:

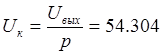 В

5. Расчет мощностей.

Мощность от источника питания:

 Вт

Мощность на нагрузке:

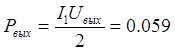 Вт

Мощность, выделяемая на коллекторе:

 Вт

КПД:                                            %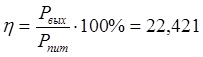

Задание10.2   Дано: на вход модулятора подается напряжение:  В. На выходе необходимо получить АМ сигнал:  В.

Параметры:

u	0	0.1	0.15	0.2	0.25	0.3	0.35	0.4	0.45	0.5	0.55	0.6
i	0	0	0.5	1	2.5	4.5	8	12	18	25	34	45

В; В; ; рад/с; рад/с; Ом.

1. Построить ВАХ НЭ, рассчитать коэффициенты аппроксимирующей функции.

Аппроксимируем данную ВАХ квадратным полиномом вида:

Составим систему уравнений:

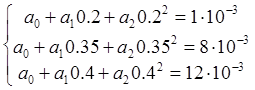
Решив систему линейных уравнений получаем:

2. Рассчитать и построить статическую модуляционную характеристику:

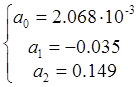
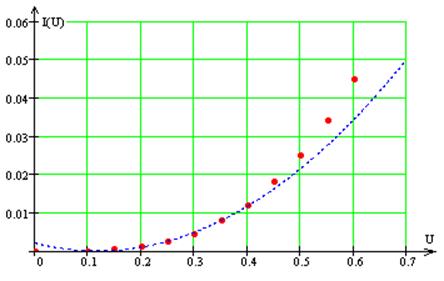
Так как на промежутках от 0 до 0.2 В  и от 0.4 до 0.6 В. аппроксимирующая функция имеет погрешность, то статическую модуляционную характеристику будем строить по трем ординатам. На промежутке от 0.2 до 0.4 В. модуляционная характеристика будет вести себя линейно, так как она наиболее приближена к реальной ВАХ:

Таким образом получаем

3. Выбор рабочей точки и максимальной амплитуды модулирующего напряжения.

                                                           

                     

                                   

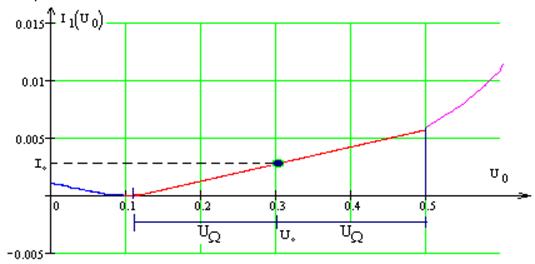
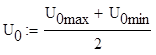
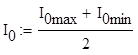
Коэффициент модуляции по току

                     

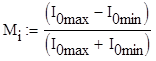
Амплитуда модулирующего напряжения:

                   

4. Графики.

5. Спектр тока на выходе НЭ.

6. Определить параметры контура

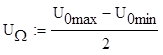
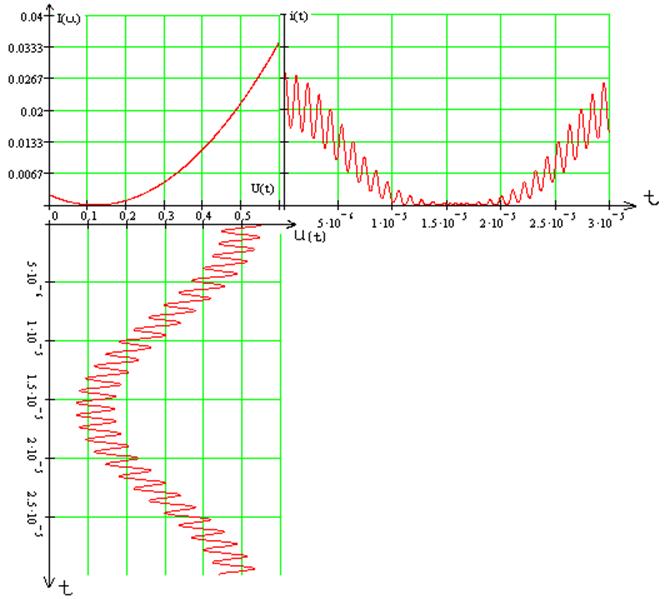
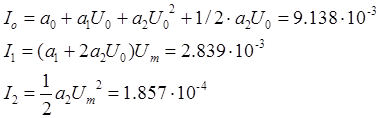
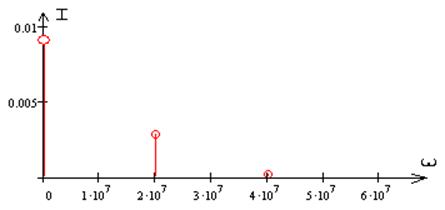
Найдем резонансное сопротивление контура:

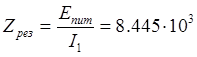Ом

Найдем характеристическое сопротивление:

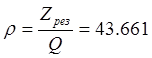Ом

(Q вычисляется из отношения)

Индуктивность контура?

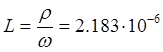Гн

Емкость контура:

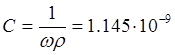Ф

Фазовый сдвиг:

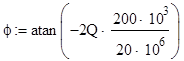
                                        град

7. Рассчитать коэффициент включения.

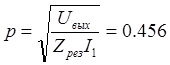
ВЫВОД   в результате всех вычислений мы получили на выходе АМ колебание

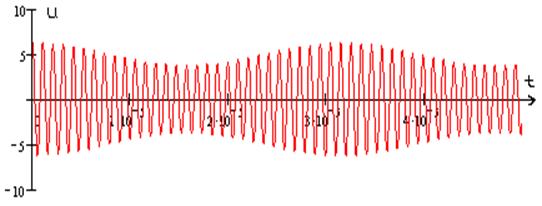
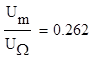
Полученный коэффициент модуляции по напряжению отличается от заданного на 1.2%.

Контур обеспечивает допустимые линейные искажения  <30%, так как коэффициент модуляции по току М=1