Генерирование гармонических колебаний, страница 2

Условия самовозбуждения

,    ,     и   .                             (11.3)

Величины вносимых сопротивлений найдем из (11.2)

.

Отсюда

                                 и       .                              (11.4)

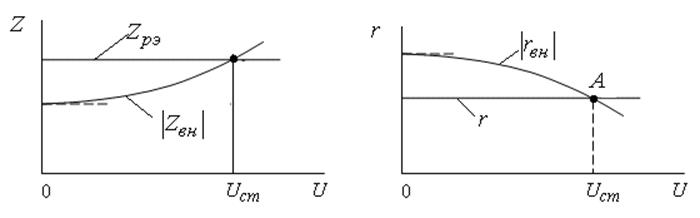
Рис. 11.8

В стационарном режиме неравенства (11.3) переходят в равенства (рис.11.8), но вместо дифференциальной крутизны  должна использоваться средняя крутизна , поскольку контур  выделяет первую гармонику возбуждаемого колебания

11.3. Дифференциальное уравнение генератора.

         Режим самовозбуждения (линейный режим)

Обратимся к схеме рис. 11.7,а и представим её в виде, изображенном на рис. 11.9.

Ток в узле А (или В) равен нулю, т.е.

.

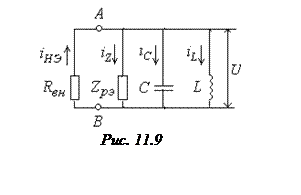
Выразим все токи через напряжение на контуре

.

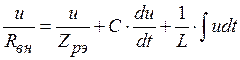Продифференцируем это интегродифференциальное уравнение и поделим на , тогда

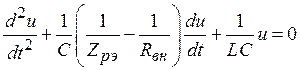           .                            (11.5)        

          Это уравнение в общем случае нелинейное, т.к. коэффициент при первой производной зависит от искомой переменной . Действительно

и. Нелинейность уравнения является следствием наличия в схеме НЭ с нелинейными функциями и .

В режиме самовозбуждения амплитуда возникающих колебаний мала и уравнение (11.5) может рассматриваться как линейное с  крутизной и внутренним сопротивлением НЭ в рабочей точке:  и .

          Характеристическое уравнение

, где

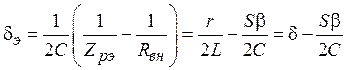                          и 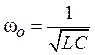                       (11.6)

–  эквивалентный коэффициент затухания и резонансная частота контура. Согласно критерию Рауса-Гурвица для устойчивой системы необходимо, чтобы все коэффициенты характеристического уравнения были положительными. Отрицательным может быть только коэффициент . Следовательно, система неустойчива когда .

Запишем корни характеристического уравнения

, где

                                                                                (11.7)

- частота свободных колебаний. Решение уравнения (11.5) запишется в виде

,                    (11.8)

где – амплитуда, зависящая от начальных условий.

Зависимость характера колебаний от  показана на рис. 11.10.

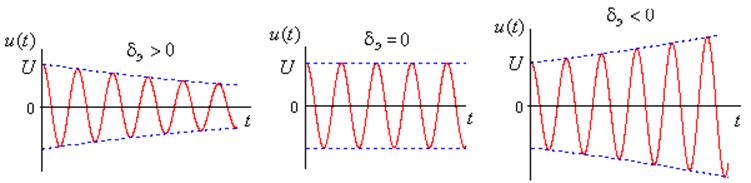
Рис. 11.10

Таким образом,  условие самовозбуждения генератора запишется в виде:

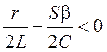                              или  ,   , .                          (11.9)

А в  соответствии с критерием Найквиста (как уже ранее указывалось) оно выражается

            

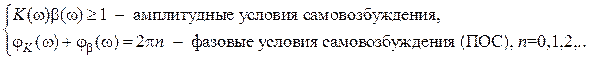
В критическом режиме

                  (11.10)

Получить критический режим можно, меняя различные параметры системы (…) В частности крутизну можно изменять напряжением смещения   на НЭ, а резонансное сопротивление контура – с помощью переменного сопротивления шунта , подключенного параллельно контуру.            

11.4. Стационарный режим (нелинейный)

В этом режиме нарастающие автоколебания попадают в область нелинейности параметров АЭ (отсечка, ограничение). Их рост замедляется и прекращается. Наступает стационарный режим. При этом  и  становятся функциями амплитуды и частоты, а условия самовозбуждения (11.3) переходят в уравнения баланса.

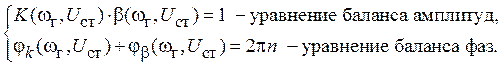                       (11.11)

Совместное решение уравнений баланса позволяет вычислить значения стационарной частоты и амплитуды АК (). Расчет существенно упрощается, если  не зависят от амплитуды АК. Тогда из уравнения баланса фаз получаем .

Будем считать АГ гармонических колебаний узкополосной системой. Это позволяет воспользоваться выводами квазилинейной теории (раздел 05) для расчета характеристик и параметров АГ. С учетом условия баланса амплитуд (11.11) имеем

, ,                          (11.12) 

                                                          (11.13)

Колебательная характеристика  и зависимость  могут быть сняты  экспериментально или построены по заданной или аппроксимированной ВАХ  НЭ (например, с использованием метода трех ординат).

Для аналитического определения амплитуды стационарных АК аппроксимируем ВАХ НЭ, например, полиномом

, где , или