Умножение частоты

6. УМНОЖЕНИЕ ЧАСТОТЫ

Умножение частоты широко используется в различной аппаратуре и, в том числе, радиопередающих устройствах. Дело в том, что в передатчиках серьезным требованием является стабильность частоты. Поэтому высокая стабильность частоты обеспечивается в задающем генераторе за счет применения кварцевого резонатора. А так как толщина пластины кварцевого резонатора обратно пропорциональна частоте, то  из соображений конструктивной реализуемости резонатора частота задающего генератора выбирается относительно невысокой (не более 10 - 20 МГц), примерно на порядок меньшей рабочей частоты передатчика. В последующих каскадах передатчика осуществляется умножение частоты. Оно применяется и в измерительных приборах, где требуется получить «сетку» частот, кратных опорной частоте.

          6.1. Резонансный умножитель частоты

Эта операция аналогична резонансному усилению (рис. 5.1). Разница заключается в том, что контур ЛП настраивается на -ю гармонику входного сигнала (). При этом будут справедливы основные формулы расчета нелинейного резонансного усилителя, в которых необходимо заменить напряжения, токи и параметры по первой гармонике соответствующими параметрами по -й гармонике.

Амплитуда напряжения на выходе умножителя рассчитывается по формуле

   .                                       (6.1)

Из (6.1) следует, что при  и ,  полностью определяется соответствующей функцией Берга , которая (рис.  2.5) достигает максимума при оптимальном угле отсечки

.                                  (6.2)

Если величина импульса тока  на выходе нелинейного элемента сохраняется постоянной (а для этого одновременно с изменением смещения  необходимо изменять и , т.е. =), то для расчета  удобнее использовать коэффициенты . В этом случае

.                              (6.3)

Коэффициент гармоник на выходе умножителя может быть рассчитан по формуле (5.12). При этом под корнем будут амплитуды всех гармоник, кроме -й, а в знаменателе амплитуда -й гармоники. При расчете всех остальных параметров и характеристик умножителя используются те же выражения, что и в усилителе, но с заменой  на .

Таким образом, для умножения частоты характерны режимы работы с большими амплитудами входного сигнала.

Основные факторы, ограничивающие  порядок умножения частоты в одном каскаде

Во-первых,  при повышении порядка  умножения происходит уменьшение амплитуды тока  и, следовательно, полезной мощности  из-за убывания коэффициента . При этом для сохранения амплитуды  импульса тока   неизменной,  оптимальный угол осечки обеспечивается при большей амплитуде входного напряжения .

Во-вторых, с ростом  ухудшается форма выходного сигнала, она может сильно отличаться от синусоидальной. Резонансная частота контура , а его полоса пропускания . При постоянной добротности  с ростом порядка умножения  полоса расширяется и в нее попадают соседние гармоники тока (рис. 6.1).

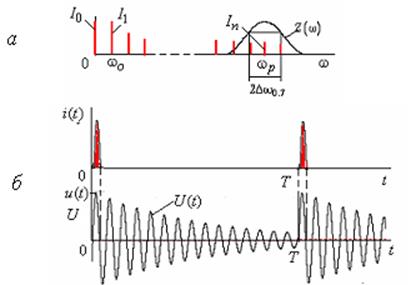
Рис. 6.1

В этих случаях  напряжение на контуре нагляднее  определять из рассмотрения свободных колебаний, возбуждаемых каждым из импульсов тока.  В промежутке  между импульсами тока укладывается  периодов свободных колебаний, и амплитуда напряжения на выходе изменяется по закону

,                                             (6.4)

где – коэффициент затухания контура.

По этим причинам подобные умножители используются лишь для умножения в 2-3 раза. 

          6.2. Другие подходы умножения частоты

1. Схема умножения частоты в большое число раз

Она представлена на рис. 5.8 и содержит нелинейный каскад – формирователь импульсов (ФИ) и фильтр (Ф).

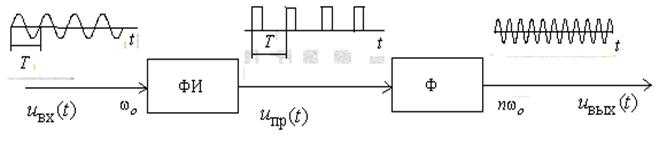
Рис. 6.2

С помощью ФИ гармонический сигнал  заданной частоты  превращается в периодическую последовательность коротких прямоугольных импульсов  той же частоты. Амплитуды спектральных составляющих последовательности медленно убывают с ростом  (рис. 6.3),  и тем медленнее, чем больше скважность импульсов . В этом случае устраняется первый из указанных выше факторов ограничения, но не второй, ибо при выделении фильтром нужной гармоники  частоты по-прежнему сказывается влияние соседних гармоник.

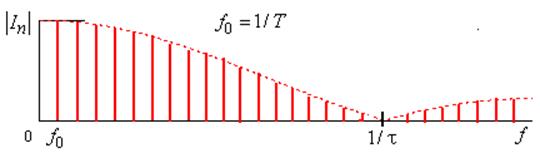
Рис. 6.3

Для получения «сетки» из  частот потребуется использовать  полосовых фильтров на выходе ФИ. Качественная фильтрация проблематична из-за относительно близкого расположения соседних гармоник.

2. Использование АПС

При объединении входов (рис. 6.4) перемножитель возводит в квадрат приложенное к ним напряжение.

Если  , то

   .                       (6.5)

При использовании в качестве фильтра разделительного конденсатора (или фильтра верхних частот – ФВЧ) на ее выходе получим напряжение с удвоенной частотой, определяемое вторым слагаемым выражения (6.5).

Рис. 6.4

В схеме, изображенной на рис. 6.4, умножение происходит в  раз, где  – количество АПС.

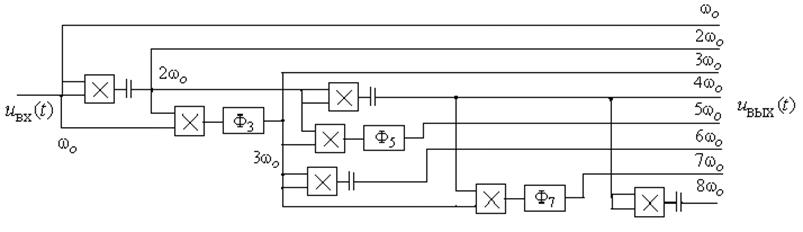
Рис. 6.5

Для получения «сетки» частот схема усложняется. В качестве примера на рис.6.5 приведена схема для «сетки» из восьми составляющих. Здесь  – полосовой фильтр для выделения суммарной -ой составляющей на выходе соответствующего АПС, при этом Разностная составляющая на выходе перемножителя отстоит от выделяемой относительно далеко и тем дальше, чем выше порядок умножения.

          3. Использование реактивных элементов

Умножение частоты возможно с помощью реактивных управляемых  (параметрических) элементов, например основанных на емкости -перехода полупроводникового диода. Такие диоды называются варикапами. Варактором  называется варикап, предназначенный для работы на СВЧ. В режиме умножения частоты он выделяет значительную мощность [Г-2].

6.3. Задача синтеза умножителя

Умножение частоты является одной из немногих задач, которые полностью решаются как задачи синтеза. В этом случае в результате решения требуется найти характеристику НЭ, с помощью которого можно осуществить умножение в заданное число раз с единственной составляющей полезной частоты .

Входной сигнал гармонической формы

.

Найдем обратную функцию

       , где  – нормированное значение входного сигнала.

Выходной сигнал – ток НЭ должен являться -ой гармоникой частоты

       .

Подставляем в это выражение полученное ранее значение , получаем

или переходя к нормированной переменной , имеем

.                                          (6.6)

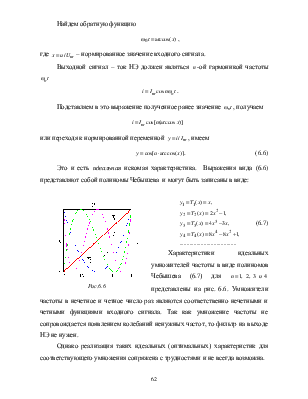
Это и есть идеальная искомая характеристика.  Выражения вида (6.6) представляют собой полиномы Чебышева  и могут быть записаны в виде:

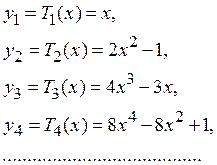         (6.7)

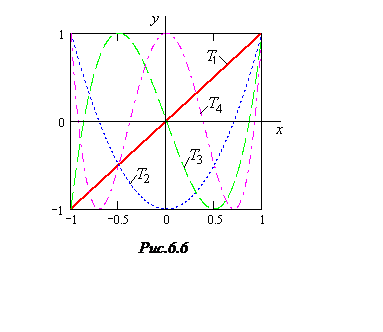
Характеристики идеальных умножителей частоты в виде полиномов Чебышева (6.7) для  представлены на рис. 6.6. Умножители частоты в нечетное и четное число раз являются соответственно нечетными и четными функциями входного сигнала. Так как умножение частоты не сопровождается появлением колебаний ненужных частот, то фильтр на выходе НЭ не нужен.

Однако реализация таких идеальных (оптимальных) характеристик для соответствующего умножения сопряжена с трудностями и не всегда возможна.