Расчет снижения мощности сигнала при отсутствии амплитудных флюктуаций

При какой средней мощности флюктуирующего радиоимпульса со случайной фазой длительностью 1 мкс может быть получена вероятность правильного обнаружения 0,85, если СПМ помехи составляет Вт/Гц, а вероятность ложной тревоги 10^–7? Во сколько раз можно снизить мощность сигнала при отсутствии амплитудных флюктуаций?

Решение

На практике неизвестной является не только начальная фаза, но и амплитуда. В этом случае используется следующая модель сигнала [1]:

,                                                      (1)

где параметр а, определяющий амплитуду сигнала, является случайным и распределенным по закону Релея с дисперсией :

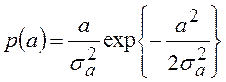.                                                                       (2)

Фаза сигнала (1) распределена по равномерному закону . Учитывая, что значения  и  статистически независимы, можно записать выражение для отношения правдоподобия [2-4]:

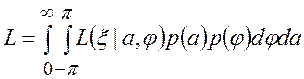.                                                          (3)

Подставляя сюда 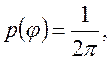  и выражение для условного отношения правдоподобия, имеем:

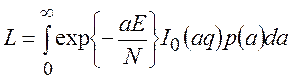.                                                                 где энергия сигнала  соответствует значению 1.

Далее, используя (2) и интеграл:

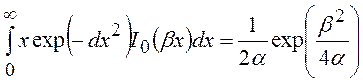,                                                     получаем:

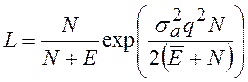,                                                                    (4)

где  - усредненная энергия сигнала.

Поскольку 0 отношение правдоподобия (4) является монотонной функцией , поэтому алгоритм оптимального обнаружителя определяется выражением

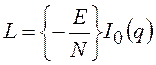,                                                                                  (5)

где  - модифицированная функция Бесселя нулевого порядка и, следовательно, структура приемника-обнаружителя сигналов со случайной амплитудой и начальной фазой аналогична структуре приемника-обнаружителя сигналов со случайной начальной фазой.

Вероятность правильного обнаружения определяется выражением:

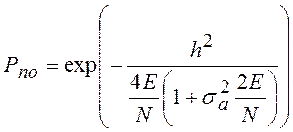,                                                            (6)

а вероятность ложной тревоги определяется выражением

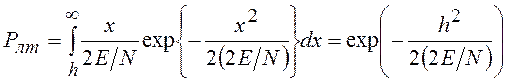                        (7)

Полагаем, что построим зависимости (6) и (7) в Wolfram Mathematica (интересующие нас кривые построенные штрих-пунктиром рис.1)

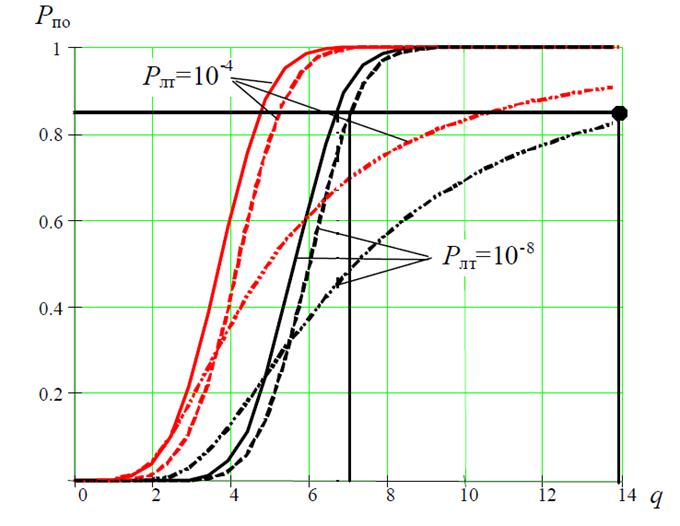
Рис.1

,

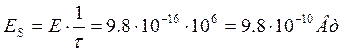
В случае отсутствии амплитудных флюктуаций

Начальная фаза сигнала, как правило, неизвестна. В этом случае можно использовать модель сигнала [1]:

,                                                           (8)

где законы амплитудной  и фазовой  модуляций и частота  известны, а начальная фаза  неизвестна.

Выражение (8) удобно представить в виде:

,                                                         (9)

где: ,  - квадратурные составляющие сигнала.

Начальная фаза сигнала предполагается равномерно распределенной случайной величиной в интервале :

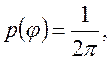
 .                                                                     (10)

Отношение правдоподобия  в рассматриваемой задаче получается путем усреднения условного отношения правдоподобия  по всем возможным значениям фазы [3-4]:

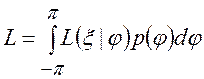.                                                                         (11)

Условное отношение правдоподобия  совпадает с отношением правдоподобия для детерминированного сигнала, у которого значение начальной фазы известно, поэтому:

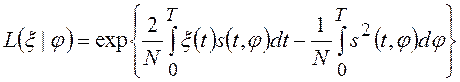.                              (12)

Подставив в (12) выражение (9), получим:

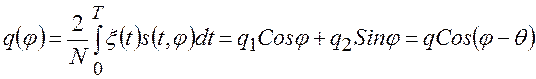,                  (13)

где: 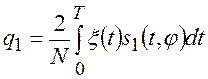,  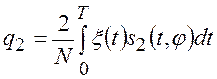- квадратурные составляющие; , , .

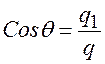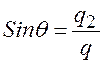При 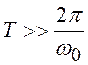 энергия сигнала  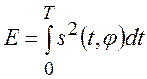от значения фазы практически на зависит и поэтому:

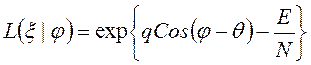.                                                       (14)

Подставляя это выражение и (10) в (11), получаем отношение правдоподобия:

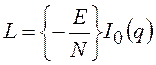,                                                                                 (15)

где  - модифицированная функция Бесселя нулевого порядка.

Так как огибающая шума и смеси сигнала с шумом на выходе обнаружителя распределена по закону Релея и обобщенному закону Релея (закону Райса) соответственно, то вероятности ложной тревоги и правильного обнаружения для обнаружителя, работающего по алгоритму (15), имеют вид:

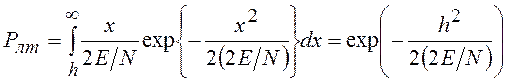,                       (16)

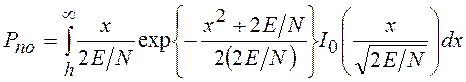,                             (17)

где .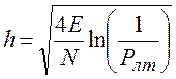

Полагаем, что построим зависимости (16) и (17) в Wolfram Mathematica (интересующие нас кривые построенные пунктиром рис.1)

,

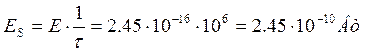
В 4 раза можно снизить мощность сигнала при отсутствии амплитудных флюктуаций .

Литература

1. Тихонов В.И. Оптимальный прием сигналов. – М.: Радио и связь, 1983.

2. Сосулин Ю.Г. Теоретические основы радиолокации и радионавигации: Учебное пособие для вузов. – М.: Радио и связь, 1992.

3. Прием и обработка сигналов в авиационных радиоустройствах /под ред. В.В. Криницына. - М.: Транспорт, 1992.

4. Калмыков В.В., Кузнецов А.А., Сенин А.И. Оптимальные методы приема сигналов. - М.: МГТУ им. Н.Э. Баумана, 1995.