Схема оптимального обнаружителя пачки из 4 когерентных радиоимпульсов

Задача 2.9 (2.11)

Привести схему оптимального обнаружителя пачки из 4 когерентных радиоимпульсов, начальные фазы которых:  неизвестна,   ,  , .

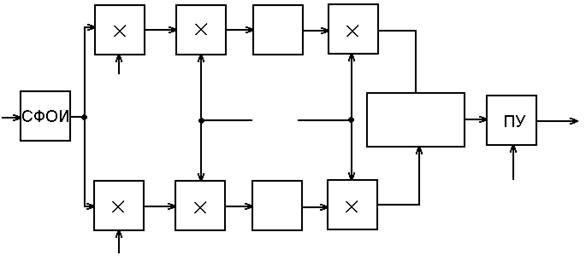
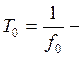 период несущей радиоимпульса.

 длительность одиночного импульса.

накапливающий сумматор N выборочных значений( и ), опрашиваемый в момент окончания наблюдений(конца пакета) .

комплексные амплитуды, описывающие известный закон модуляции амплитуд и фаз.

Задача 2.24(2,26) Обнаруживаемый сигнал описывается соотношением

 В,         , где

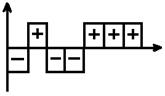
- случайная величина, а огибающая  принимает значения +1 и –1 в соответствии с кодом «», причём длительность одного элемента составляет . При какой интенсивности помехи типа белый шум вероятностей ложной тревоги и правильного обнаружения будут равны и 0,9 соответственно? Изобразить схему обнаружителя и определить порог.

Решение:

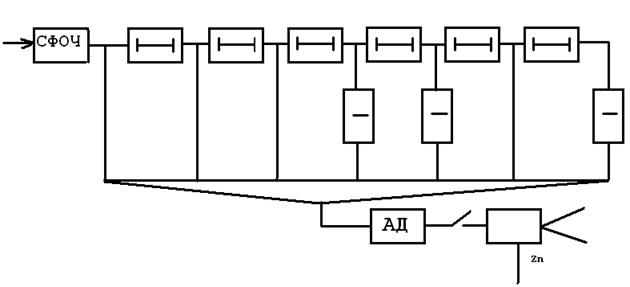
   При   

 (0,55 дБ)-  потери в пороговом устройстве связанные со случайным характером фазы

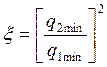
- ОСШ необходимое для обнаружения сигнала с вероятностями  и  со случайной начальной фазой.

- ОСШ необходимое для детектирования сигнала.

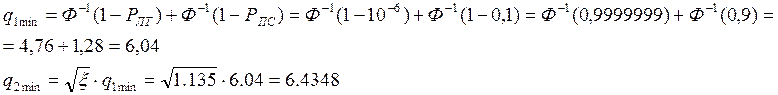
Энергия сигнала: 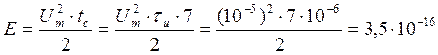 Вт.

т.к. 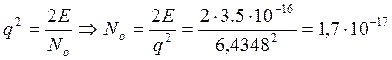Вт/Гц

Нормируемый порог:  

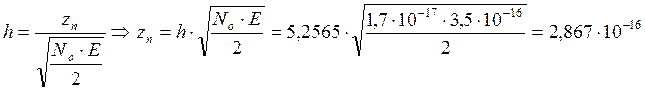
Задача 2.44 (2,42)

При обнаружении когерентной пачки из двух импульсов с одмнаковыми амплитудами при настроенном приемнике получены вероятности правильного обнаружения 0.95 и ложной тревоги    . Из-за нестабильности начальная фаза второго импульса неконтролируемо изменяется на . Найти зависимости F и D от  .

Решение:

На рис.1 приведена функциональная схема приемника.

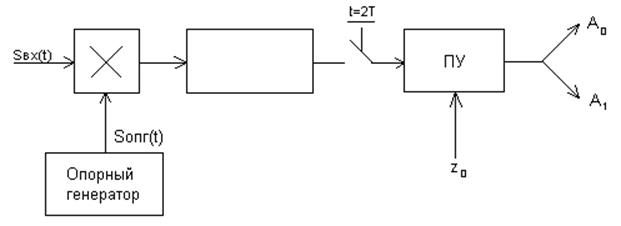
рис.1:Корреляционный приемник Котельникова.

ü  Запишем выражения для входного сигнала и сигнала с опорного генератора:

;

; Случайное изменение фазы на величину

;

т.е. в умножителе перемножаются две косинусоиды с различными значениями начальных фаз.

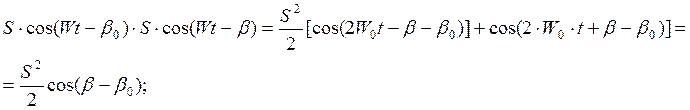
Корреляционный интеграл:

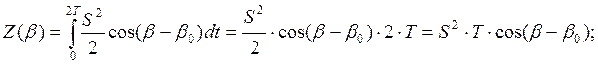
При S=1 и при   

Вероятность ложной тревоги определяется выражением: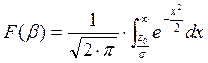 

Вероятность правильного обнаружения определяется выражением:

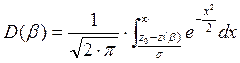
Для получения зависимостей требуемых в условии необходимо найти  и .

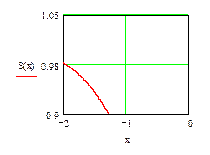
Чтобы найти значения этих характеристик воспользуемся интегралом вероятности.

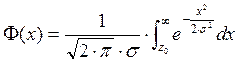
Сделаем замену переменных: =>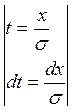  

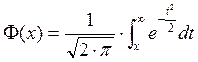
ü  По кривой интеграла вероятности находим x где 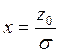 для случая :

    

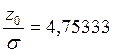
По кривой интеграла вероятности находим x где 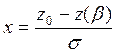 для случая :

  

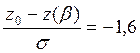
При несмещенной фазе(начальное условие) равной нулю и условно принятого нами T=1   получаем систему уравнений:

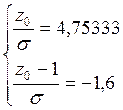В результате решения данной системы получаем:  

Результаты подставляем в ниже приведенные выражения, причем предел интегрирования со стороны бесконечности  для удобства вычислений заменяем определенным числом, например числом 20.

Вероятность ложной тревоги: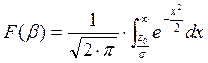 

Вероятность правильного обнаружения: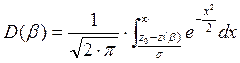

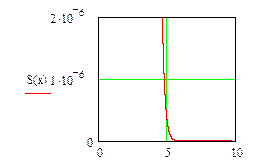
Построим эти зависимости, причем уже из формулы определения вероятности ложной тревоги, видно, что от фазы она не зависит и представляет из себя определенную const.

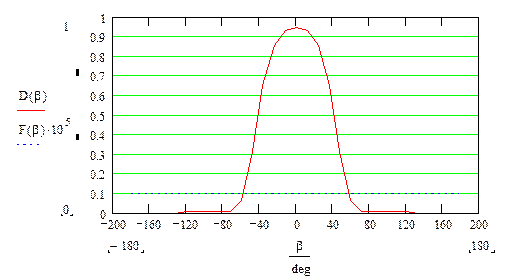
Графики зависимостей вероятностей от фазы второго импульса когерентной пачки.

Задача 2.86 (2,94)

Дискретная независимая выборка  принадлежит экспоненциальному распределению 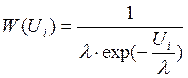; , содержащему неизвестный параметр  . Определить значение  оценки максимального правдоподобия, а также найти смещение и дисперсию этой оценки . Сопоставить дисперсию с нижней границей, определяемой неравенством Крамера-Рао, и сделать вывод об эффективности оценки. 

Найдем совместную плотность распределения вероятности , так как выборка независима она равна.

               ;

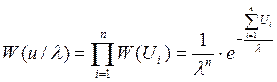
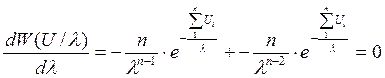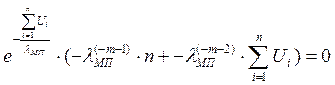
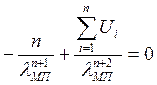
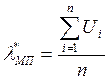
ü  Проверим оценку на несмещенность: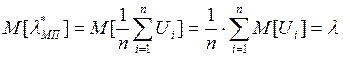

Отсюда, делаем, вывод—оценка является несмещенной.

ü  Найдем дисперсию оценки: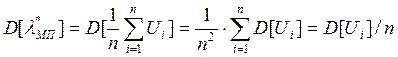

ü  Сравним дисперсию с нижней границей определяемой неравенством  Крамера-Рао:

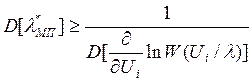
Для несмещенной оценки при большом числе выборки, т.е. при  неравенство, приведенное выше, превращается в равенство. Таким  образом, при бесконечно большом n,  дисперсия оценки совпадает с нижней границей Крамера-Рао.

ü  Эффективность оценки:

Полученная оценка ,которая обращает неравенство Крамера-Рао в равенство,  называется эффективной.

Задача 2.87 (2,95)   

Азимут маневрирующей цели описывается стахостатическим разностным уравнением  град., в котором дискретное время; информационный гауссовский шум с параметрами . В результате работы пеленгатора формируются первичные измерения:, содержащие некоррелированный гауссовский шум измерений  с дисперсией  и нулевым средним. Записать алгоритм фильтра Калмана, осуществляющего вторичную обработку (сглаживание) измерений. Определить дисперсию сглаженных оценок и найти выигрыш в точности, обусловленный сглаживанием, как в динамике так и в установившемся состоянии.

Решение:

Запишем уравнение наблюдения: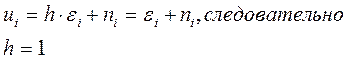

Запишем уравнение сообщения:

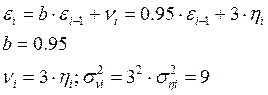
Задача 2.88 (2,102)

Дальность цели изменяется по закону: , км; , где  - информационный белый шум, , . ,  - независимый гауссовский шум. Получаемая в результате оценка дальности имеет дисперсию км². Найти алгоритм сжатия и дисперсию шума .

Решение

1)         , где  - в общем случае

 - сообщение,  - наблюдение. Исходя из этого, можно записать: , причем ,

; , где , а

2)         Имеем формулу:

Для нашего случая это выглядит так: ; ; ; ;  - неизвестное.

Получаем:       ;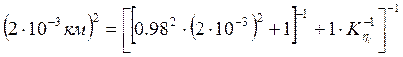

;

;

;

;

;

.

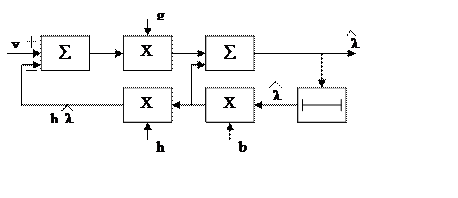
Ответ: