Исследование дискретизации сигналов

Лабораторная работа № 1

Исследование дискретизации сигналов

Цель работы

Ознакомиться с принципом выбора частоты дискретизации непрерывного сообщения, механизмом возникновения ошибок при дискретизации.

Описание работы

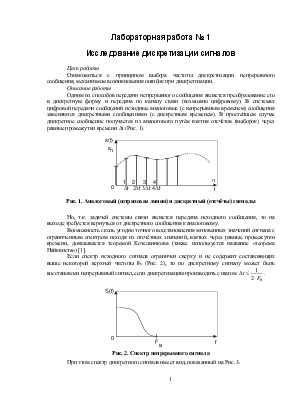
Одним из способов передачи непрерывного сообщения является преобразование его в дискретную форму и передача по каналу связи (возможно цифровому). В системах цифровой передачи сообщений исходные аналоговые (с непрерывным временем) сообщения заменяются дискретными сообщениями (с дискретным временем). В простейшем случае дискретное сообщение получается из аналогового путём взятия отсчётов (выборок) через равные промежутки времени Dt (Рис. 1).

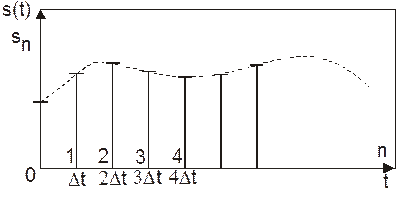
Рис. 1. Аналоговый (штриховая линия) и дискретный (отсчёты) сигналы

Но, т.к. задачей системы связи является передача исходного сообщения, то на выходе требуется вернуться от дискретного сообщения к аналоговому.

Возможность сколь угодно точного восстановления мгновенных значений сигнала с ограниченным спектром исходя из отсчётных значений, взятых через равные промежутки времени, доказывается теоремой Котельникова (также используется название «теорема Найквиста») [1].

Если спектр исходного сигнала ограничен сверху и не содержит составляющих выше некоторой верхней частоты F_в (Рис. 2), то по дискретному сигналу может быть восстановлен непрерывный сигнал, если дискретизацию производить с шагом .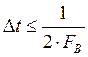

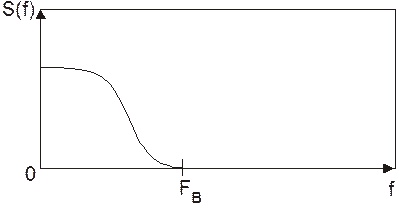
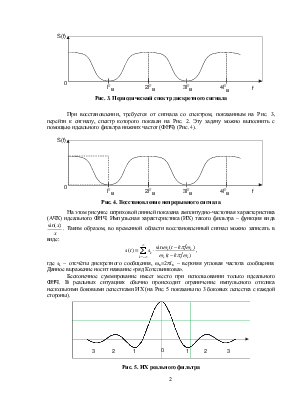
Рис. 2. Спектр непрерывного сигнала

При этом спектр дискретного сигнала имеет вид, показанный на Рис. 3.

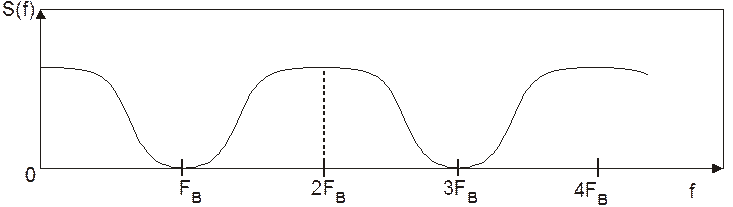
Рис. 3. Периодический спектр дискретного сигнала

При восстановлении, требуется от сигнала со спектром, показанным на Рис. 3, перейти к сигналу, спектр которого показан на Рис. 2. Эту задачу можно выполнить с помощью идеального фильтра нижних частот (ФНЧ) (Рис. 4).

Рис. 4. Восстановление непрерывного сигнала

На этом рисунке штриховой линией показана амплитудно-частотная характеристика (АЧХ) идеального ФНЧ. Импульсная характеристика (ИХ) такого фильтра – функция вида 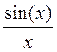. Таким образом, во временной области восстановленный сигнал можно записать в виде:

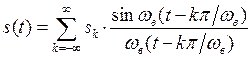, где s_k – отсчёты дискретного сообщения, w_в=2pf_в – верхняя угловая частота сообщения. Данное выражение носит название «ряд Котельникова».

Бесконечное суммирование имеет место при использовании только идеального ФНЧ. В реальных ситуациях обычно происходит ограничение импульсного отклика несколькими боковыми лепестками ИХ (на Рис. 5 показаны по 3 боковых лепестка с каждой стороны).

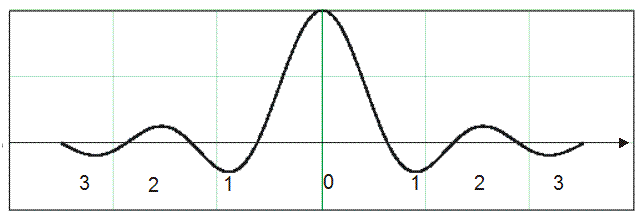
Рис. 5. ИХ реального фильтра

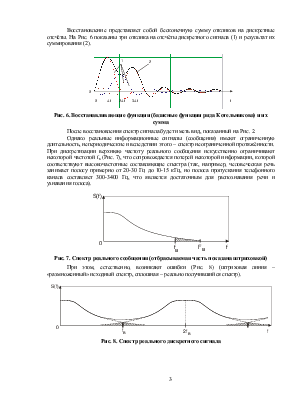
Восстановление представляет собой бесконечную сумму откликов на дискретные отсчёты. На Рис. 6 показаны три отклика на отсчёты дискретного сигнала (1) и результат их суммирования (2).

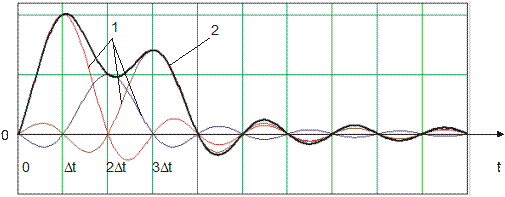
Рис. 6. Восстанавливающие функции (базисные функции ряда Котельникова) и их сумма

После восстановления спектр сигнала будет иметь вид, показанный на Рис. 2.

Однако реальные информационные сигналы (сообщения) имеют ограниченную длительность, непериодические и вследствии этого – спектр неограниченной протяжённости. При дискретизации верхнюю частоту реального сообщения искусственно ограничивают некоторой частотой f_в (Рис. 7), что сопровождается потерей некоторой информации, которой соответствуют высокочастотные составляющие спектра (так, например, человеческая речь занимает полосу примерно от 20-30 Гц до 10-15 кГц, но полоса пропускания телефонного канала составляет 300-3400 Гц, что является достаточным для распознавания речи и узнавания голоса).

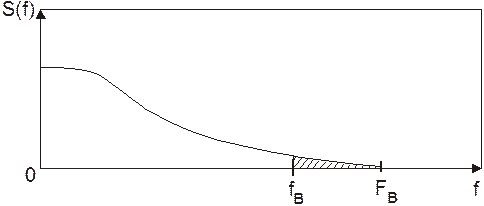
Рис. 7. Спектр реального сообщения (отбрасываемая часть показана штриховкой)

При этом, естественно, возникают ошибки (Рис. 8) (штриховая линия – «размноженный» исходный спектр, сплошная – реально получившийся спектр).

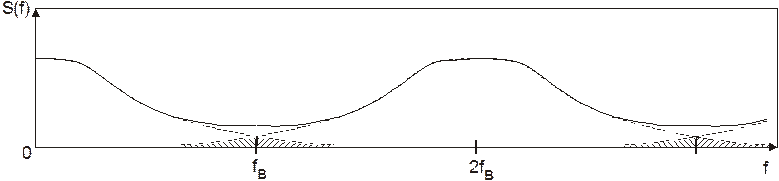
Рис. 8. Спектр реального дискретного сигнала

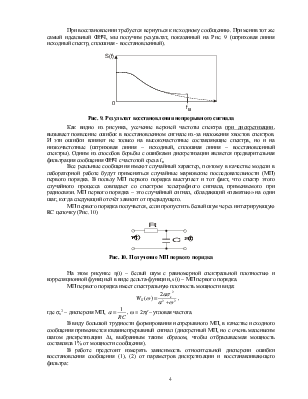
При восстановлении требуется вернуться к исходному сообщению. Применив тот же самый идеальный ФНЧ, мы получим результат, показанный на Рис. 9 (штриховая линия исходный спектр, сплошная - восстановленный).

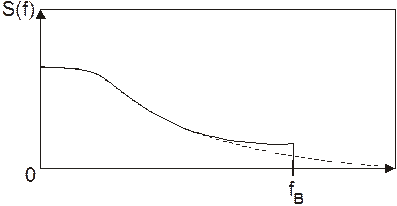
Рис. 9. Результат восстановления непрерывного сигнала

Как видно из рисунка, усечение верхней частоты спектра при дискретизации, вызывает появление ошибок в восстановленном сигнале из-за наложения хвостов спектров. И эти ошибки влияют не только на высокочастотные составляющие спектра, но и на низкочастотные (штриховая линия – исходный, сплошная линия – восстановленный спектры). Одним из способов борьбы с ошибками дискретизации является предварительная фильтрация сообщения ФНЧ с частотой среза f_в.

Все реальные сообщения имеют случайный характер, поэтому в качестве модели в лабораторной работе будут применяться случайные марковские последовательности (МП) первого порядка. В пользу МП первого порядка выступает и тот факт, что спектр этого случайного процесса совпадает со спектром телеграфного сигнала, применяемого при радиосвязи. МП первого порядка – это случайный сигнал, обладающий «памятью» на один шаг, когда следующий отсчёт зависит от предыдущего.

МП первого порядка получается, если пропустить белый шум через интегрирующую RC цепочку (Рис. 10)

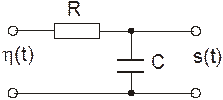
Рис. 10. Получение МП первого порядка

На этом рисунке h(t) – белый шум с равномерной спектральной плотностью и корреляционной функцией в виде дельта-функции, s(t) – МП первого порядка.