Цель работы:
Ознакомиться с методами обработки прямых равнорассеянных измерений и получить практические навыки по их использованию.
1.Генерирование случайных чисел
а) Нормальное(Гауссово) распределение
Величина y имеет нормальное распределение,. плотность вероятности задается выражением
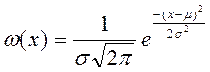
Зададимся следующими параметрами:
Количество
измерений ![]()
Мат.
ожидание ![]()
СКО ![]()
|
|
|
|
График плотности распределения
Построим гистограмму. Гистограмма представляет собой столбцовую диаграмму, высота каждого столбца которой определяется частотой попадания выборочных значений в соответствующий интервал. Гистограмма является эмпирическим, или выборочным, аналогом таблицы или плотности распределения.
|
|
Как видно из графика, гистограмма по форме практически совпадает с графиком плотности распределения, что говорит о правильности построения.
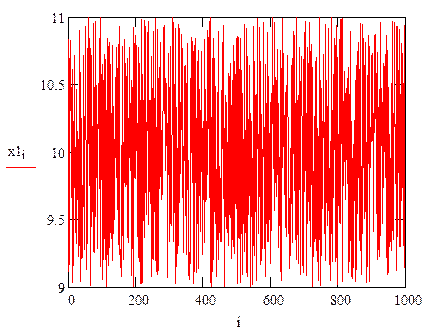
б)Равномерное распределение
Равномерное распределение - плотность вероятности равна постоянна на заданном интервале наблюдения.
Интервал наблюдения: ![]()
![]()
![]()
Плотность распределения:
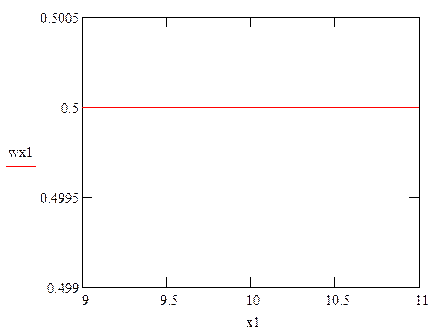
Гистограмма:
|
|
в) Распределение Стьюдента
Если x1,x2…xn распределены по нормальному закону, то величина
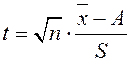 (1)
(1)
распределена по закону Стьюдента с (n-1)-ой степенью свободы, плотность вероятности которого:
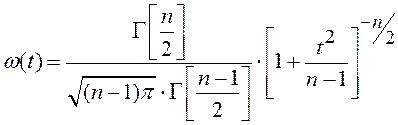 (2)
(2)
в (1) и (2) ![]() ;
; 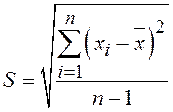 ;
; ![]() - гамма функция. Величину S2 называют выборочной дисперсией совокупности величин x1,x2…xn.
- гамма функция. Величину S2 называют выборочной дисперсией совокупности величин x1,x2…xn.
![]()
![]()
![]()
|
|
|
|
График плотности распределения
Гистограмма:
|
|
2. Зависимость мат. ожидания и дисперсии от количества измерений.
Мат. ожидание и дисперсия для всех 3х случаев вычисляем по формуле:
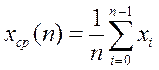 .
.
Дисперсия по формуле:
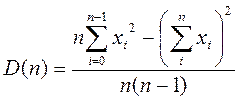
Построим графики зависимостей:
А) Нормальное распределение
|
|
|
|
Б) Равномерное распределение
|
|
|
|
В)
|
|
|
|
Как видно, при увеличении количества измерений мат.ожидание и дисперсия всё больше начинают стремиться к некоторой постоянной величине.
В случае А)Нормального распределения xср с увеличением числа измерений приближается к постоянной величине, равной μ=10, заданной ранее.
В случае Б) равномерного распределения, как можно видеть из
графика плотности распределения, среднее значение x должно быть равным 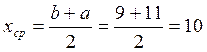 . Это
подтверждается графиком зависимости мат.ожидания от количества измерений.
. Это
подтверждается графиком зависимости мат.ожидания от количества измерений.
В случае В) распределения Стьюдента мат.ожидание равно 0.
3) Рассчитать вероятности попадания случайной величины х в интервал 9..1 для данных распределений.
А) Нормальное распределение:
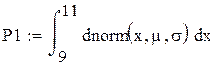
![]()
Вероятность очень велика – 95,4%. Это объясняется тем, что мат.ожидание в данном распределении равно 10 и плотность распределения сосредоточена в данном интервале (9…11).
Б) Равномерное распределение
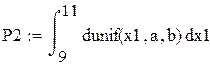
![]()
Вероятность попадания в данный интервал равна 100%, т.к. случ.величина равномерно распределена на интервале 9…11.
В) распределение Стьюдента.
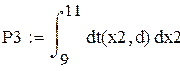
![]()
Вероятность стремится к 0, т.к.плотность распределения вероятности сосредоточена ок 0,в интервале -5…5. Это подтверждается значением вероятности:
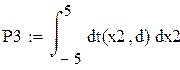
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.