Рассчет равновероятного интервала при равномерном законе распределения погрешностей, рассчет истинного среднеквадратического значения напряжения сигнала

Задача № 1.1,б.

При измерении частоты сигнала  были получены следующие результаты наблюдений : , , , , , , , , , кГц.

Считать, что генеральная совокупность отклонений результатов наблюдений распределена по нормальному закону.

Определить: результат измерения частоты , значение среднеквадратического отклонения результатов наблюдений  (исключить, если имеются промахи), значение среднеквадратической погрешности результата измерения , указать его доверительную вероятность ; интервал случайных погрешностей  с доверительной вероятностью .

·  Рассчет результата измерения частоты .

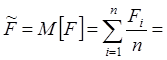
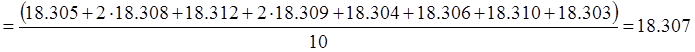кГц.

·  Рассчет среднеквадратического отклонения результатов наблюдений .

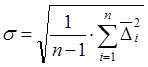, где  – абсолютная погрешность -го измерения.

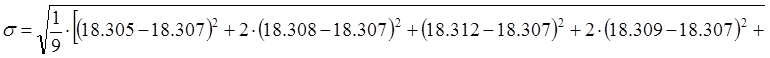
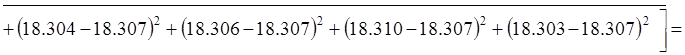
кГц.

С целью установления промахов воспользуемся правилом «трех сигма» – если , то такой результат не является промахом. . Результаты вычислений представлены в таблице 1.

Таблица 1

, кГц	18.305	18.308	18.312	18.309	18.304	18.306	18.310	18.303
, кГц	0.006	0.008	0.004	0.007	0.005	0.007	0.006	0.004

Т.к. во всех случаях выражение  больше нуля, то можно заключить, что грубых погрешностей нет.

·  Рассчет среднеквадратической погрешности результата измерения .

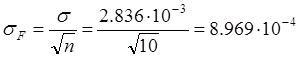кГц.

·  Рассчет доверительной вероятности .

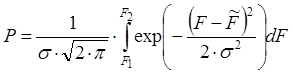, где , .

После замены 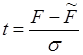 получаем следующее:

.

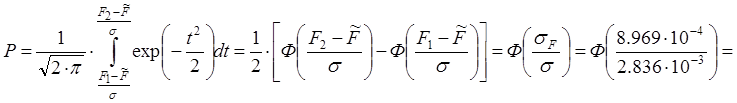
·  Рассчет равновероятного интервала случайных погрешностей.

Т.к. число измерений мало (), то для нахождения интервала случайных погрешностей воспользуемся распределением Стьюдента, согласно которому . Для заданных доверительной вероятности  и числа наблюдений , табулированное значение коэффициента Стьюдента . Следовательно:

кГц.

Задача № 1.6.

Проведено измерение частоты кГц с погрешностью в интервале кГц с доверительной вероятностью .

Чему равны равновероятные интервалы  () при равномерном и нормальном законах распределения случайных погрешностей?

·  Рассчет равновероятного интервала при равномерном законе распределения погрешностей:

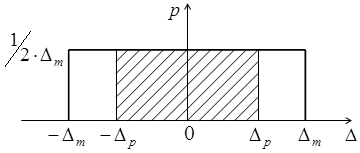Все возможные случайные погрешности результата измерений расположены в интервале , где  – максимальная погрешность. Вероятность того, что случайная величина  попадет в интервал , равна .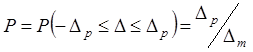

Рисунок 1 – График равномерного закона распределения плотности вероятности.

Из условия задачи известно, что такая вероятность  при . Следовательно, кГц. Тогда для вероятности :

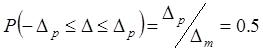, и интервал кГц.

·  Рассчет равновероятного интервала при нормальном законе распределения погрешностей:

Из условия задачи известно, что , где  – табулированный интеграл вероятностей, 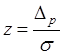, кГц. Находим , соответствующее вероятности : 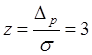, тогда 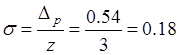кГц.

Следовательно, для вероятности :

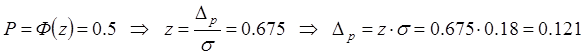кГц.

Задача № 2.9.

Вольтметрами магнитоэлектрической, электромагнитной и электростатической систем измеряется напряжение

.

Что покажет каждый вольтметр, с какой абсолютной погрешностью , если классы точности каждого , пределы измерения от  до В?

·  Рассчет показаний вольтметров.

Вольтметр магнитоэлектрической системы покажет , т.к. может измерять только постоянное напряжение. Вольтметры же двух других систем (электромагнитной и электростатической) измеряют действующее значение и дадут следующее показание:

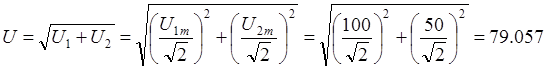В.

·  Рассчет абсолютной погрешности .

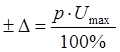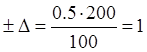, где % – класс точности прибора, В – предел измерения. Тогда получаем, что В.

Задача № 2.12.

Электронный вольтметр подгруппы ВЗ имеет амплитудный преобразователь, открытый вход, шкала его калибрована в среднеквадратическом значении напряжения гармонического сигнала.

При подаче на него сигнала с ,  он показал по шкале В. Чему равно истинное среднеквадратическое значение напряжения сигнала?

·  Рассчет истинного среднеквадратического значения напряжения сигнала.

Т.к. шкала этого вольтметра градуирована не в амплитудных, а в среднеквадратических значениях 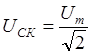 гармонического сигнала, то действительное значение амплитуды входного напряжения равно В. Тогда истинное среднеквадратическое значение напряжения сигнала равно:

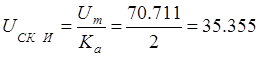В.

Задача № 3.2.

Универсальный осциллограф подгруппы С1 имеет коэффициент отклонения мВ/См, коэффициент развертки мкс/см, частоту развертки кГц, время развертки мкс.

Нарисуйте наблюдаемое изображение сигнала в виде квазипрямоугольного импульса с параметрами: мВ, частотой следования кГц, длительностью импульса мкс, длительностью фронтов мкс (влиянием частотной полосы осциллографа можно пренебречь).

·  Рассчет геометрических размеров изображения импульса на экране