Значит, если вы введете вещественное число (в круглых скобках или без них) на место комплексных переменных a или b, то это интерпретируется как комплексная переменная с нулевой мнимой частью. Для ввода же переменной с = 3.14 –1.0j, необходимо в круглых скобках через запятую ввести отдельно действительную и мнимую части.
Операторы класса complex
Комплексные числа можно складывать, вычитать, умножать, делить, сравнивать,
#include <complex>.
complex< double > a;
complex< double > b;
complex< double > с = a * b + a / b;
Комплексные и арифметические типы разрешается смешивать в одном выражении:
complex< double > a;
complex< double > d = a + 3.14159;
Внимание! В правой части приведенного оператора происходит суммировние комплексной переменной и вещественной константы. Тип этих объектов должен быть одинаковым, в данном случае – это double, так как константа с десятичной точкой в Visual C++ имеет по умолчанию тип double. Если же типы этих объектов не совпадут, то компилятор выдаст ошибку:
complex< float > a;
complex< double > d = a + 3.14159;//ОШИБКА
Устраним эту ошибку
complex< float > a;
complex< double > d = a + 3.14159f; //OK
Буква f в конце числа сообщает компилятору, что тип числа – float.
Класс комплексных чисел поддерживает четыре составных оператора присваивания: +=, -=, *= и /=. Таким образом, если
complex <float>a,d; то можно записать
a+=d;
Функции для работы с комплексными числами
Класс complex имеет две функции, возвращающие соответственно вещественную и мнимую части. Мы можем обращаться к ним, используя синтаксис доступа к членам класса:
complex<double> z;
double re = z.real();
double im = z.imag();
или эквивалентный синтаксис вызова функции:
double re = real(z);
double im = imag(z);
Кроме того, для работы с комплексными числами имеются следующие функции: abs(), arg(), conj(), polar(), sqrt(), sin(), cos(), tan(), exp(), log(), log10() и pow(). Функция polar() по модулю и аргументу комплексного числа находит его действительную и мнимую части, функция conj(z) возвращает комплексно сопряженное число к числу z.
1. Написать, ввести и отладить программу вычисления переменных a или b в соответствии с вариантом. Предусмотреть вывод исходных данных и результатов на экран монитора.
2. Используя формулу для смешанного соединения сопротивлений, найти выражение для сопротивления z между узлами а и б схемы, изображенной на рис. 1.2. Создать программу расчета вещественной и мнимой части этого сопротивления, а также его модуля и аргумента. Исходные данные для расчета взять из табл. 1.2.
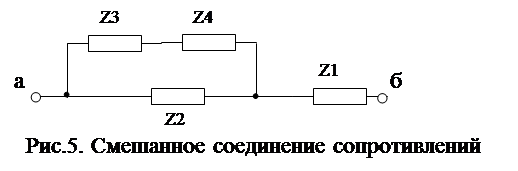 |
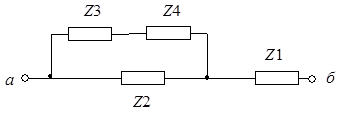
Рис. 1.2. Смешанное соединение сопротивлений
Таблица 1.2
|
Вариант |
Z1 |
Z2 |
Z3 |
Z4 |
||||
|
real |
imag |
real |
imag |
real |
imag |
real |
imag |
|
|
1 |
3 |
0 |
3.14159 |
4.08 |
5 |
9 |
0 |
2.1 |
|
2 |
6.28 |
1.414 |
0 |
6 |
4.1 |
12 |
2.7 |
0 |
|
3 |
0 |
0 |
3 |
4 |
3.14159 |
2.0009 |
2.1 |
4.14 |
|
7 |
8.45 |
4 |
8.87465 |
–2.2 |
0 |
5 |
2.71 |
–5 |
|
5 |
–4 |
–5 |
8.2 |
0 |
4.1 |
3.8 |
–7.12 |
0 |
|
6 |
–9.13 |
0.5 |
6 |
7 |
0 |
0 |
8 |
2 |
|
7 |
0 |
–7.2 |
4.14 |
3 |
12 |
8 |
6.7 |
8.13 |
|
8 |
6.128 |
8 |
0 |
6.87 |
6.456 |
–0.9 |
6 |
9 |
|
9 |
–8.37 |
0 |
4 |
5 |
7.19 |
5 |
0 |
–0.07 |
|
10 |
1.41454 |
3.2 |
7.2 |
–0.787 |
6 |
0 |
6.12 |
6 |
|
11 |
2 |
3 |
6.23456 |
0 |
8.123 |
–7.5 |
–4 |
13.6 |
|
12 |
4.12 |
–0.654 |
5 |
3 |
7.12345 |
0 |
7.13 |
4.414 |
|
13 |
0 |
2 |
–4.24 |
0 |
8 |
8.12345 |
–6.2 |
5.1 |
|
14 |
–2 |
–4 |
4.41487 |
–5.1 |
4.765 |
3 |
0 |
4.34 |
|
15 |
0 |
0 |
5.567 |
–7.4 |
2.12345 |
–3.1 |
2 |
3 |
3. Оформить отчет по работе, обратив особое внимание на выводы. Подготовиться к защите, ориентируясь на контрольные вопросы. Защитить работу.
Даны x,
y. Вычислить 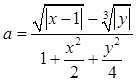 .
.
Даны x,
z. Вычислить ![]() .
.
Даны x,
y, z. Вычислить 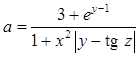 .
.
Даны x,
y. Вычислить 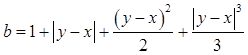 .
.
Даны x,
y. Вычислить 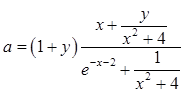 .
.
Даны x,
y, z. Вычислить 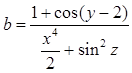 .
.
Даны x,
y. Вычислить 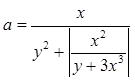 .
.
Дано z.
Вычислить 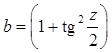 .
.
Даны x,
y. Вычислить 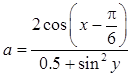 .
.
Дано z.
Вычислить 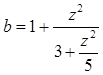 .
.
Даны x,
y. Вычислить 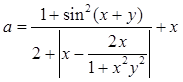 .
.
Дано z.
Вычислить 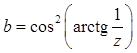 .
.
Даны x,
y, z. Вычислить 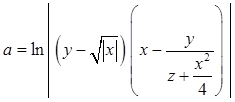 .
.
Дано x.
Вычислить 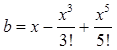 .
.
Даны гипотенуза и катет прямоугольного треугольника. Найти второй катет и угол между найденным катетом и гипотенузой.
Известна длина окружности. Найти площадь круга, ограниченного этой окружностью.
Вычислить период колебания маятника длиной l.
Найти площадь кольца, внутренний радиус которого равен 20, а внешний – заданному числу R (R > 20).
Найти площадь равнобочной трапеции с основаниями a и b (a > b) и углом a при большем основании.
Дано действительное число x. Не пользуясь никакими другими арифметическими операциями, кроме умножения, сложения и вычитания, вычислить 2x4 – 3x3 + 4x2 – 5x+ 6. Разрешается использовать не более четырех умножений и четырех сложений и вычитаний.
Даны действительные числа c, d, x1, x2. Вычислить
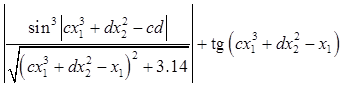 .
.
Найти сумму членов арифметической прогрессии a, a + d, …, a + (n–1)d; a, d, n задать с клавиатуры компьютера.
Дана длина ребра куба. Найти объем куба и площадь его боковой поверхности.
Даны катеты прямоугольного треугольника. Найти его гипотенузу и площадь.
Дано действительное число a. Не пользуясь никакими другими арифметическими операциями, кроме умножения, получить a8 за 3 операции.
Дано действительное число h. Вычислить
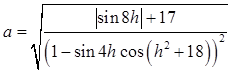 .
.
Дано действительное число h. Вычислить
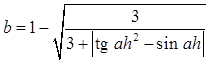 .
.
Дано действительное число h. Вычислить ![]() .
.
Вычислить 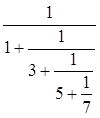 .
.
Дано действительное число x. Вычислить 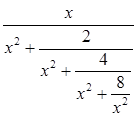 .
.
1. Дайте определение арифметического выражения.
2. Каков порядок выполнения арифметического выражения?
Перевести с С++ на математический язык: A/B*C , A/B/C.
Не привлекая компьютер, рассчитать n:
int y=21,a=2,b=3,n; float c=4; n= -a++*b/a*a/c*b;
3. Каким образом можно вывести информацию на экран?
Число 1.414213562 было выведено на экран в виде xxxx1.4142. Как при этом должен выглядеть оператор вывода?
4. Каков диапазон представления констант различных типов? Сколько значащих десятичных цифр могут содержать константы разных типов?
6. Как организовать пробел, перевести строку при выводе информации?
7. Каков смысл во вводе чисел с клавиатуры при исполнении программы?
9. Как объявить комплексную переменную двойной точности?
10. Как ввести с клавиатуры комплексную переменную z = 1.414 + 2j?
1. Изучение методов организации разветвляющихся и циклических вычислительных процессов.
2. Приобретение навыков программирования разветвляющихся и циклических вычислительных процессов при работе с одномерными массивами.
Во многих случаях последовательность выполнения операторов программы не может быть однозначно определена до начала расчетов. Часто выбор следующего действия зависит от значения некоторого
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.