Излучение радиоволн уединенными элементарными антеннами. Электромагнитное поле элементарного электрического диполя (диполя Герца)

1. ИЗЛУЧЕНИЕ РАДИОВОЛН УЕДИНЕННЫМИ

ЭЛЕМЕНТАРНЫМИ АНТЕННАМИ

1.1. Общие положения

Произвольная излучающая система может рассматриваться как совокупность некоторого числа достаточно простых по структуре излучателей, поля которых интерферируют и формируют излучение всей системы. Это позволяет воспользоваться принципом суперпозиции и определить итоговое электромагнитное поле всей системы как векторную сумму полей более простых излучателей [1, 2]. Процедура оценивания свойств электромагнитного поля таких излучателей имеет ряд особенностей, которые целесообразно прокомментировать на конкретных примерах часто используемых элементарных излучателей. Этот материал будет необходим при компьютерном моделировании реальных печатных излучателей, так как позволяет грамотно сформировать адекватную топологию «начального приближения» таких широко распространенных антенн, как дипольные, щелевые, кардиоидные, турникетные, директорные, логопериодические и т.п.

1.2. Электромагнитное поле элементарного электрического диполя (диполя Герца)

Диполь Герца представляет собой тонкий цилиндрический, короткий по сравнению с длиной волны проводник. Вдоль проводника протекает высокочастотный ток, амплитуда которого не изменяется вдоль длины проводника . Особенности технической реализации такого режима возбуждения короткого проводника изучаются в курсе лекций по дисциплине «Устройства СВЧ и антенны».

Поместим диполь в начало сферической системы координат и ориентируем его вдоль оси  (орт , рис. 1.1). Объемное распределение плотности тока проводимости в диполе запишем в виде (здесь и далее верхняя «точка» и нижний индекс  в обозначениях комплексных амплитуд опускаются с целью сокращения записи)

.         (1.1)

При этом составляющими  и 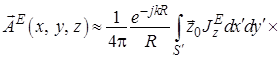 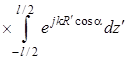 мы пренебрегаем из-за того, что поперечное сечение  диполя является весьма малым [3]. Тогда составляющие запаздывающего векторного электродинамического потенциала  (по англоязычной терминологии – «магнитного вектор-потенциала электрического тока») можно найти исходя из общей его записи [4]:

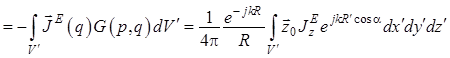,    (1.2)

где  – точка наблюдения;  – точка интегрирования;  – объем диполя Герца;  – функция Грина свободного пространства. Если учесть, что величина  весьма мала и постоянна вдоль оси , можно и дальше упростить (1.2):

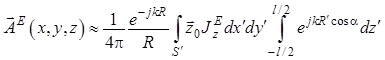.          (1.3)

Если точка наблюдения лежит в дальней зоне, то

;     ;     ;     .

Тогда (1.3) примет вид

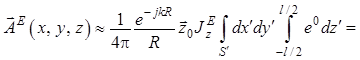
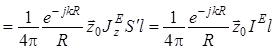,                     (1.4)

здесь  – комплексная амплитуда электрического тока, который несет на себе диполь Герца. Последнее означает, что векторный потенциал осевого электрического тока  имеет проекцию только на ось , что позволяет записать соответствующие проекции векторного потенциала

                       (1.5)

в сферической системе координат в виде:

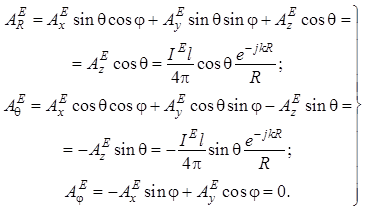             (1.6)

Далее учтем, что в общих формулах для комплексных амплитуд полей [5, 6]

,

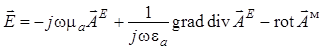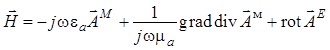
первое и второе слагаемые в выражении для  исчезают, так как диполь Герца, несущий на себе только ток проводимости (электрический ток), не создает электродинамический потенциал , обусловленный «магнитным» током, т.е.

,                                        (1.7)

где  определяется согласно предыдущим двум формулам. Для того чтобы способствовать лучшей ориентировке студентов при самостоятельной работе, целесообразно дальнейшие преобразования согласно (1.7) выполнить подробно.

Поскольку вектор  [формулы (1.5) и (1.6)] не имеет проекции на орт  и, кроме того, у него нет вариаций по углу  вследствие симметрии системы относительно оси , т. е.

,

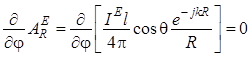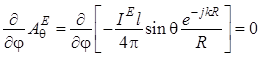,                       (1.8)

вычисления ротора согласно (1.2.7) приводят к результату:

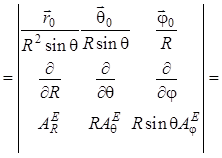
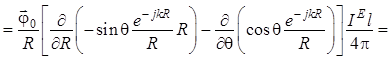
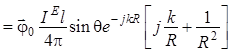.                          (1.9)

Таким образом, компоненты комплексной амплитуды векторной напряженности магнитного поля  по ортам  и  отсутствуют:

.                                     (1.10)

Далее отыскиваются составляющие комплексной амплитуды  векторной напряженности электрического поля электромагнитного излучения диполя Герца. Их можно найти из первого соотношения системы уравнений Максвелла в комплексной форме для среды без источников, т. е. для случая, когда . С учетом (1.10) будем иметь:

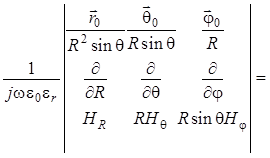
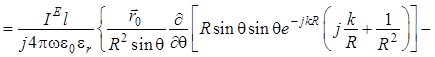
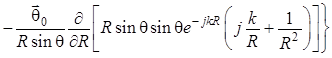.              (1.11)

Далее выполняются преобразования для отдельных составляющих. Для проекции на орт :

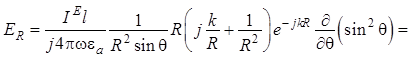
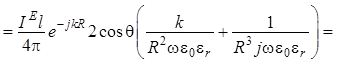
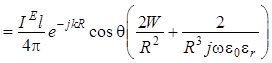.                    (1.12)

Здесь учтено, что:

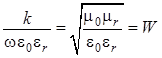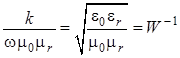, ,            (1.13)

где  – волновое сопротивление пространства в точках наблюдения .

Для проекции на орт  получаются выражения [знак минус проставлен потому, что он фигурирует в формуле (1.11)]:

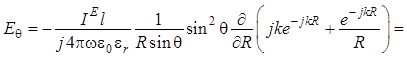
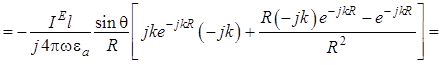
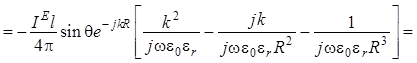
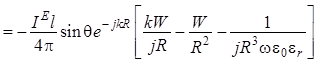.               (1.14)

Для проекции на орт  из (1.11) следует, что

.                                          (1.15)

Поскольку для точки  наблюдения, позиционированной в дальней зоне (именно дальняя зона учитывается при организации радиосвязи), выполняются неравенства  и , в полученных составляющих комплексных амплитуд векторных напряженностей полей  и  можно пренебречь слагаемыми, содержащими множители  и . Тогда из формул (1.9), (1.12) и (1.14) следует, что для диполя Герца (элементарного электрического диполя)

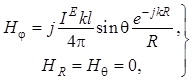                            (1.16)

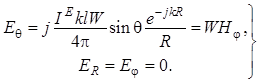                      (1.17)

Направления векторов  и  указаны на рис. 1.1.

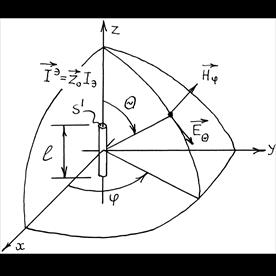
Рис. 1.1

1.3. Электромагнитное поле элементарного магнитного диполя

Элементарный магнитный диполь мыслится как тонкий цилиндрический, короткий по сравнению с длиной волны  объект, вдоль которого протекает виртуальный «магнитный» ток  с комплексной амплитудой , не изменяющейся вдоль объекта. Использование такого виртуального понятия, как «магнитный» ток, позволяет достичь высокой степени симметрии выражений для интенсивности электрического и магнитного полей  и  широко  применяется  в теории  антенных