Излучение радиоволн уединенными элементарными антеннами. Электромагнитное поле элементарного турникетного излучателя

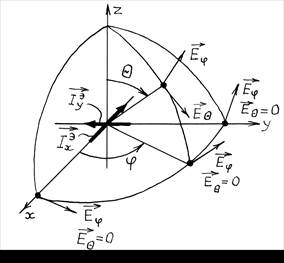
Рис. 1.5

Как и ранее, воспользуемся принципом суперпозиции и запишем комплексные амплитуды соответствующих векторных напряженностей  итогового (полного) электромагнитного поля в виде

, ,                          (1.76)

где верхние индексы x и y означают не составляющие по оси X или Y, а подчеркивают тот факт, что данная компонента поля обусловлена током  и  соответственно. Поэтому эти индексы у векторов  и выполнены верхними, а не нижними, как у токов (где они означают проекцию на соответствующую ось). Если сравнить рис. 1.3 и 1.5, то станет ясно, что для расчета составляющей  поля электрического диполя, ориентированного в сторону отрицательных значений X, можно использовать формулу (1.58) предыдущего подраздела, заменив в ней  на  :

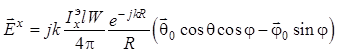.             (1.77)

Для расчета второй компоненты  полного поля  в (1.76) следует сначала найти компоненту , воспользовавшись формулой (1.49) для поля электрического диполя с учетом его ориентации в сторону отрицательных значений Y (далее в этом подразделе для сокращения записи, а также в связи с тем, что оба элементарных диполя есть диполи электрические (диполи Герца), индекс «э» опускается):

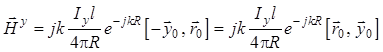.         (1.78)

С учетом второй формулы системы (1.52) можно записать:

.

Поэтому

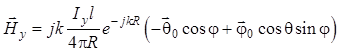.             (1.79)

Теперь составляющая  определяется из соответствующего уравнения Максвелла для среды без источников:

 .

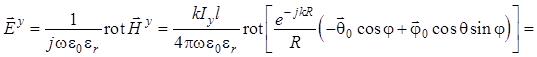
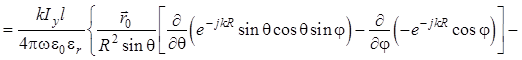
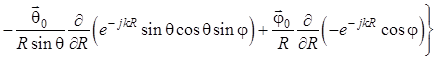Аналогично предыдущему подразделу для точек дальней зоны Фраунгофера можно пренебречь составляющими, содержащими множитель  (иными словами, в последнем уравнении исчезает проекция на орт ). Тогда может быть записано следующее уравнение:

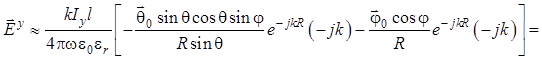
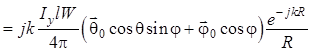.               (1.80)

В результате с учетом (1.77) и (1.80) находится комплексная амплитуда векторной напряженности  полного поля турникетного излучателя:

 

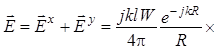
.     (1.81)

Пусть для определенности квадратурное соотношение возбуждающих токов электрических диполей имеет вид (напоминание: речь идет о комплексных амплитудах):

.                                (1.82)

Тогда составляющие полного поля

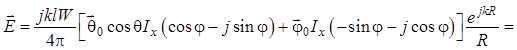
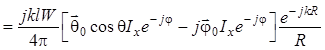
примут вид:

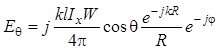,                        (1.83)

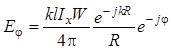.                              (1.84)

Аналогично находятся компоненты  и  формулы (1.76). Для этого в формуле (1.55) производится замена  на  , причем далее индекс Е (или Э) опускается:

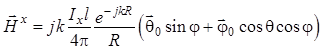.               (1.85)

Тогда с учетом (1.79) выражение для комплексной амплитуды векторной напряженности магнитного поля итогового излучения элементарного турникетного излучателя запишется:

                       

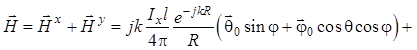
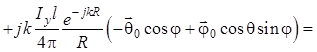
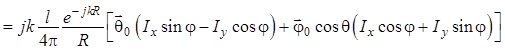. (1.86)

С учетом квадратурности (1.86) имеем:

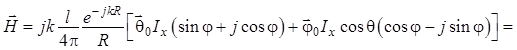
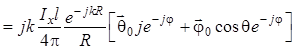.                  (1.87)

Вектор Пойнтинга определяется как

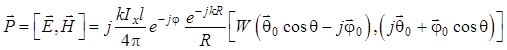. (1.88)

Среднее за период  высокочастотного колебания значение вектора Пойнтинга запишется:

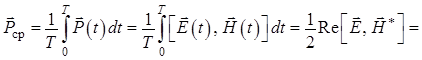
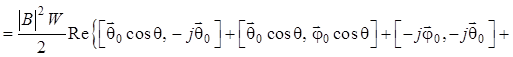
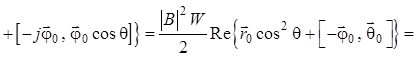
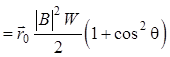,                             (1.89)

где учтено, что вещественная часть (оператор ) действительного числа равна самому этому числу, а величина  определяется как

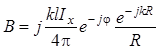.                               (1.90)

Тогда плотность потока мощности излучения  элементарного турникетного излучателя в направлении внешней нормали  к сфере очень большого радиуса  (т. е. при ) с центром в начале координат турникетного излучателя (в этом случае ) по аналогии с (1.74) запишется

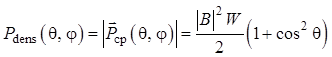.              (1.91)

Наибольшее значение плотности потока мощности будет в направлении ортов  (угол  равен нулю: ) и  (угол  равен : ) при любом угле , принимающем значения , и оно составит

.

Тогда пространственная характеристика направленности по мощности элементарного турникетного излучателя (т. е. его диаграмма направленности) определяется как

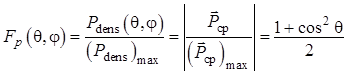.            (1.92)

Эта характеристика представляет собой тело вращения вокруг оси  и изображена на рис. 1.6.

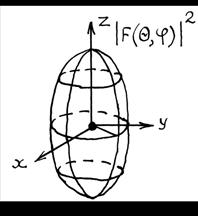
Рис. 1.6

Поляризационные свойства этого излучателя имеют ряд особенностей. Произведем их оценивание исходя из выражения для комплексной амплитуды векторной напряженности электрического поля (1.83), которое перепишем в виде

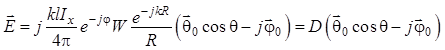.          (1.93)

Тогда мгновенное значение  будет определяться как классическая векторная гармоническая функция времени с комплексной амплитудой  [формула (1.93)]:

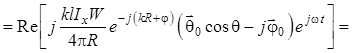
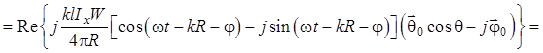
,                        (1.94)

где                             , .                         (1.95)

Таким образом, найдено, что мгновенное значение векторной гармонической функции  запишется как

,                     (1.96)

здесь

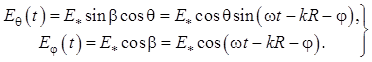           (1.97)

Рассмотрим следующие частные случаи, опираясь на формулу (1.96).

1. Плоскость  (, угол  принимает произвольные значения). Имеем:

;

 есть классическая гармоническая функция времени, соответствующая строго линейной поляризации излучения в плоскости диполей .

2. Ось  в положительном направлении (орт ; ; угол  – произвольный).

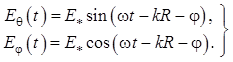
 .        (1.98)

Следовательно, геометрическое место точек концов вектора  представляет собой в пространстве цилиндрическую спираль. Ее проекция на плоскость, перпендикулярную оси , представляет собой окружность, и электромагнитная волна характеризуется круговой поляризацией.

Рассмотрим далее ситуацию, когда текущее время , и пусть при этом

,

Тогда

; .                             (1.99)

Пусть далее текущее время  увеличится на четверть периода  излучаемого высокочастотного гармонического колебания:

.                                    (1.100)

Тогда

,              (1.101)

.             (1.102)

Таким образом, можно записать:

; ; ;

; ; .             (1.103)

Поэтому, если смотреть в направлении распространения (в положительном направлении орта ), то вектор  вращается против часовой стрелки.

3. Ось  в отрицательном направлении [орт (), , угол  – любой]. При этом ,  .

Для момента времени  имеем:

; .

Для момента времени  соответственно будет

; .

Поэтому, если смотреть опять в направлении распространения (по орту ), то вектор  вращается по часовой стрелке. При этом следует подчеркнуть, что такой порядок определения направления вращения вектора  является общепринятым в теории излучения и антенн [1–6].

4. Общий случай (углы  и  принимают произвольные значения).

Из уравнения (1.97) следует:

.

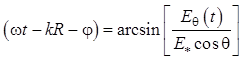Тогда

.

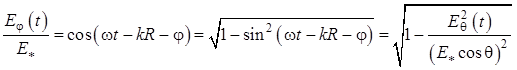Последнее уравнение можно переписать в виде

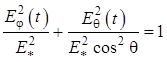.                             (1.104)

Это есть уравнение эллипса без наклона большой оси, причем проекция на орт  зависит от угла .

Таким образом, в верхней полусфере () элементарный турникетный излучатель формирует эллиптически поляризованное излучение с вращением вектора  против часовой стрелки, а в нижней полусфере () – эллиптически поляризованное излучение с вращением вектора  по часовой стрелке. Степень эллиптичности поляризации, определяемая отношением малой () и большой () полуосей поляризационного эллипса, будет принимать все возможные значения от 1 (при круговой поляризации на оси ) до нуля (при линейной поляризации в плоскости , где угол ).

1.6. Электромагнитное поле элементарных электрических и магнитных рамок (витков)

Элементарная электрическая рамка по определению представляет собой проводящий виток радиусом  (). Предполагается, что в проводнике витка, имеющем пренебрежимо малое поперечное сечение , поддерживается ток проводимости с неизменной комплексной амплитудой векторной объемной плотности  (напоминание: верхний индекс «э» здесь и далее опущен), так что . Разместим виток в плоскости XOY декартовой системы координат согласно рис. 1.7 и направим ток проводимости по орту :

.                                       (1.105)

Проанализируем структуру поля такого излучателя в дальней зоне наблюдения (зоне Фраунгофера;).