Излучение радиоволн уединенными элементарными антеннами. Электромагнитное поле элементарного магнитного диполя

устройств. При этом поперечное сечение  цилиндрического объекта считается весьма малым, а сам объект размещается (по аналогии с диполем Герца) в начале декартовой системы координат, совмещенной с соответствующей сферической системой, и ориентируется вдоль оси  (рис. 1.2).

Таким образом, принимается, что комплексная амплитуда  векторной объемной плотности магнитного тока имеет значимую составляющую только вдоль оси :

.               (1.18)

Тогда составляющие комплексной амплитуды векторного электродинамического потенциала (по англоязычной терминологии – «электрического вектор-потенциала магнитного тока») можно найти, подставив (1.18) в уравнение с функцией Грина . По аналогии с разделом 1.2 последовательно получаем:

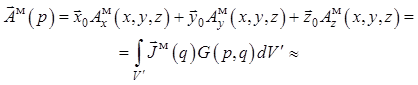
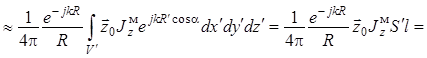
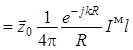,                                  (1.19)

где  – комплексная амплитуда магнитного тока, который несет на себе магнитный диполь вдоль оси .

Из последнего уравнения следует, что векторный потенциал осевого магнитного тока может быть представлен в виде

с соответствующими проекциями в сферической системе координат:

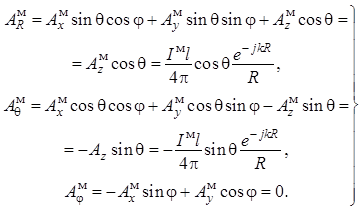            (1.20)

Далее принимаем во внимание, что магнитный диполь не создает векторный электродинамический потенциал , обусловленный электрическим током проводимости. Поэтому

.                                     (1.21)

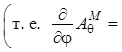
Затем учитываем, что вектор  не имеет проекции на орт  (т. е. ) и, кроме того, у него нет вариаций по углу  вследствие осевой симметрии системы относительно оси   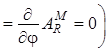. Тогда вычисления ротора (1.21) с учетом (1.20) и (1.18) дают следующий результат:

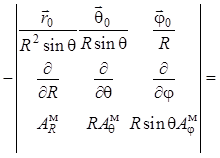
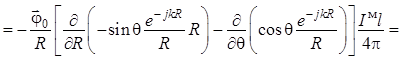
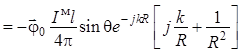.                       (1.22)

Из этого уравнения следует, что поскольку

,                                      (1.23)

компоненты комплексной амплитуды векторной напряженности  по ортам  и  отсутствуют.

Теперь определяются составляющие комплексной амплитуды векторной напряженности  излучения магнитного диполя. Их находим из второго соотношения системы уравнений Максвелла для среды без сторонних источников (сторонние источники, поддерживающие магнитный ток в магнитном диполе, существуют только внутри объема  диполя), т. е. для среды, в которой . С учетом (1.23) последовательно получаем:

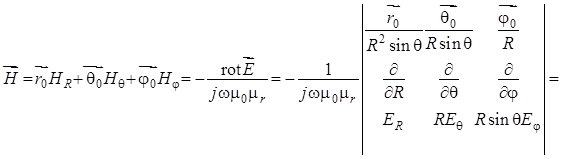
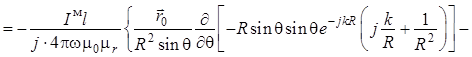
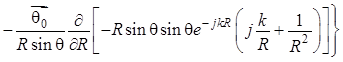.             (1.24)

Далее выполним преобразования для отдельных составляющих. Для проекции на орт :

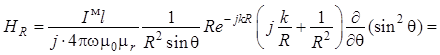
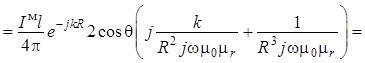
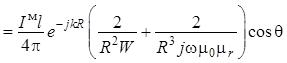,                   (1.25)

где W – волновое сопротивление (1.13) пространства в точке наблюдения.

Для проекции на орт :

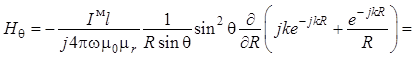
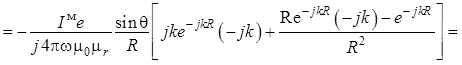
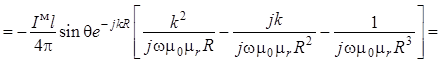
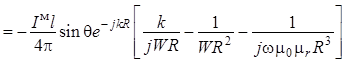.             (1.26)

Таким образом, составляющая вектора  по орту  отсутствует:

.                                        (1.27)

Поскольку для точки наблюдения в дальней зоне , в полученных выражениях составляющих векторов  и  можно пренебречь слагаемыми, содержащими множители . Тогда для магнитного диполя из формул (1.22), (1.25) и (1.26) следует, что:

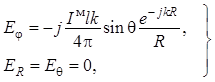                          (1.28)

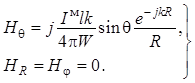                            (1.29)

Соотношения (1.28) и (1.29) определяют в полной мере структуру электромагнитного поля элементарного магнитного диполя. На рис. 1.2 показана ориентация соответствующих векторов, что следует учитывать при анализе поля более сложных излучающих систем.

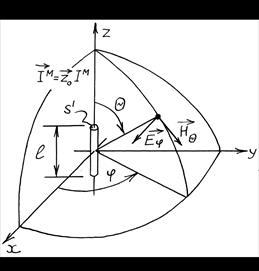
Рис. 1.2