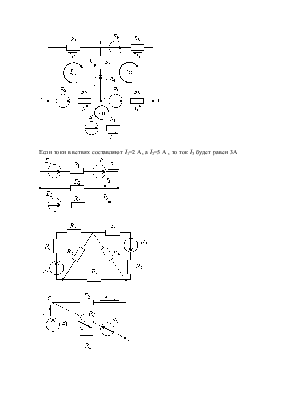




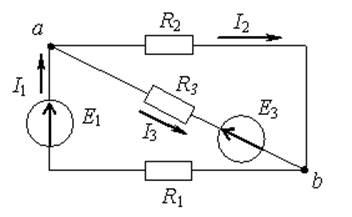
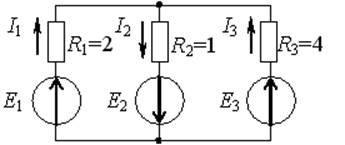
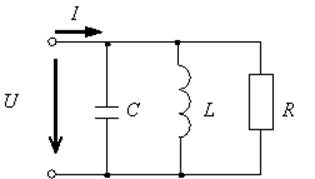
Если токи в ветвях составляют
I1=2 A, а I2=5 A , то ток I3
будет равен 3А
…
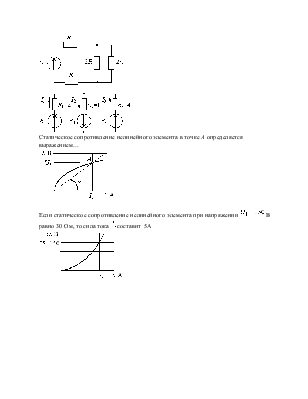
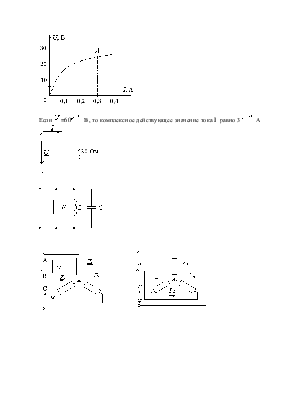
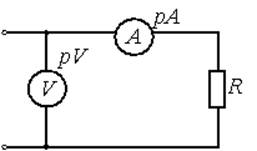
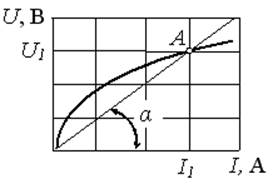
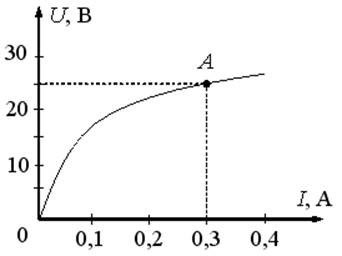
Статическое сопротивление
нелинейного элемента в точке А определяется выражением…
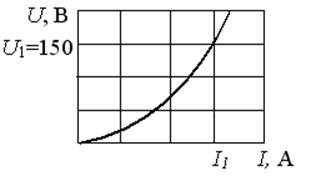
Если статическое
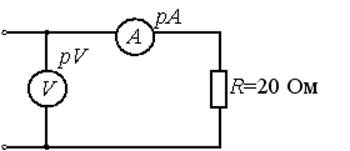
сопротивление нелинейного элемента при напряжении ![]() В равно 30 Ом, то сила тока
В равно 30 Ом, то сила тока ![]() составит 5А
составит 5А
|
1) |
|
2) |
|
|
|
3) |
|
4) |
|

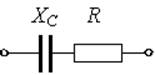
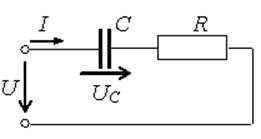
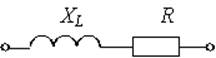
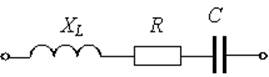
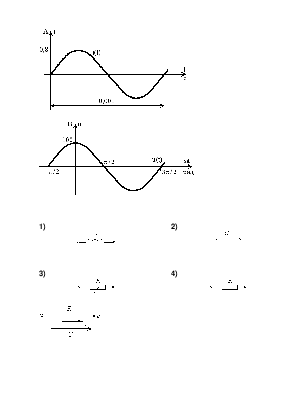
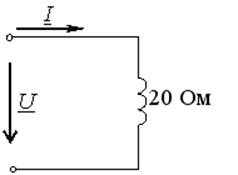
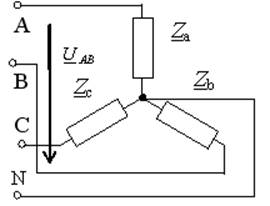
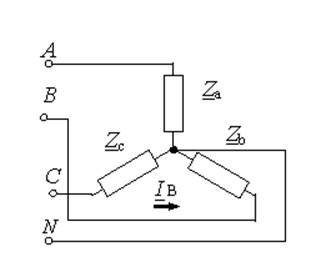
Если ![]() =60
=60![]() B, то
комплексное действующее значение тока I равно 3
B, то
комплексное действующее значение тока I равно 3![]() А
А
Электрические цепи
Цепи постоянного тока. Основные закономерности.
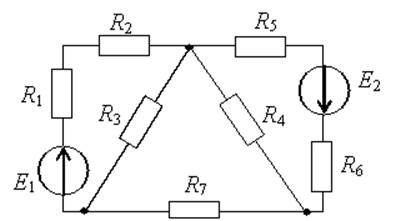
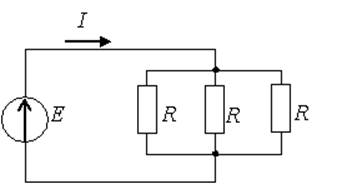
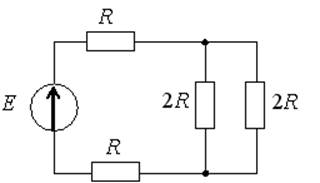
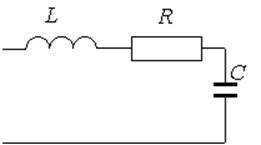
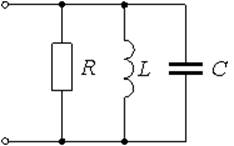
Электрическая цепь – совокупность элементов, генерирующих, потребляющих, преобразующих и передающих электрическую энергию, процессы в которых описываются понятиями ЭДС, тока, напряжения. Чтобы провести анализ и расчет, электрическую цепь представляют схемами. Схемы различают в зависимости от целей анализа: принципиальная схема, на которой изображают условными обозначениями все элементы и связи между ними (необходима для анализа принципа работы цепи); расчётная схема, на которой изображают основные характеристики и параметры элементов (необходима для расчета токов, напряжений и других величин); схема замещения, на которой реальные элементы изображают идеальными элементами замещения с такими же параметрами, характеризующими энергетические процессы; монтажная схема и пр. На рис. 1-5 приведены схемы замещения различных электрических цепей.
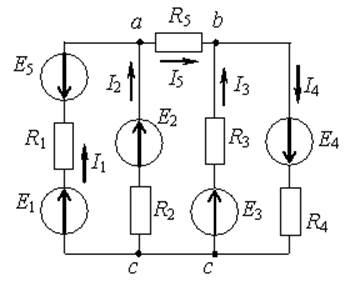

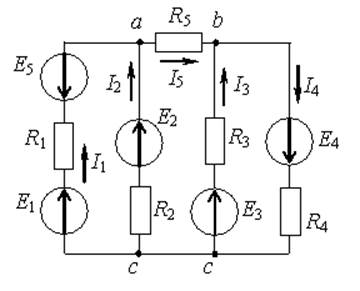
Рис. 1 Рис. 2
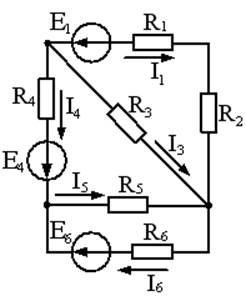
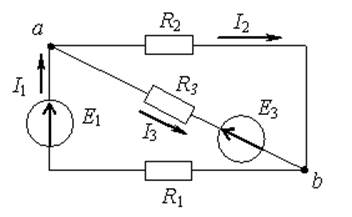
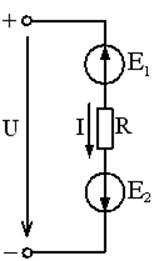
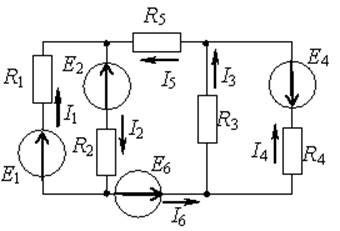
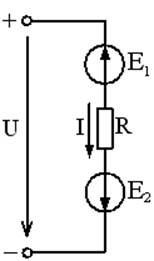
Рис. 3 Рис. 4 Рис. 5
Основные топологические понятия.
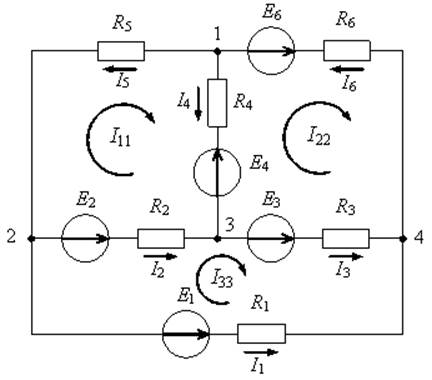
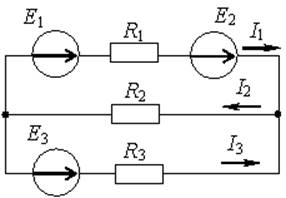
Ветвь электрической цепи – участок, по которому протекает один и тот же ток (не имеет разветвлений). Электрическая цепь, представленная на рис.1 имеет 5 ветвей (пять различных токов); на рис.2 – 6 ветвей (шесть токов); на рис. 5 – одна ветвь (один ток).
Узел – точка соединения двух и более ветвей. На рис.1 три узла (a,b,c); на рис.2 четыре узла (1,2,3,4); на рис.4 два узла (a,b).
Контур – замкнутый путь по нескольким ветвям. На рис.1,2,3 – по три, а на рис.4 - два независимых контура.
Основные законы и закономерности.
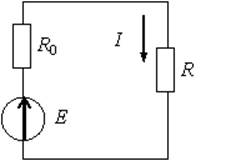
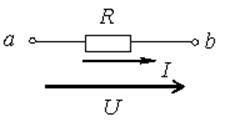
Закон Ома: I=U/R - для участка цепи;
I=E/(R+R0) – для полной цепи (рис.6)
1-й закон Кирхгофа (для узла): ∑IK=0 (сумма токов в узле равна нулю, или сумма токов, подходящих к узлу, равна сумме токов, отходящих от узла). На рис.4 для узла a
![]()
Рис.6 2-й закон Кирхгофа (для контура): ∑Ei=∑In*Rm(в замкнутом контуре сумма ЭДС E равна сумме падений напряжения на отдельных элементах R). При составлении уравнений по 2-му закону Кирхгофа выбирается произвольное направление обхода контура (например, по часовой стрелке). Если направления ЭДС E и токов I совпадают с направлением обхода, то они принимаются со знаком +, если не совпадают – принимаются со знаком минус. На рис.2 для контура 2-1-3-2 уравнение по второму закону Кирхгофа: --E2 – E4 = I2R2 + I4R4 – I5R5 ; на рис.4 для контура a-b-R1 - E1 –aуравнение запишется: E1 – E3 =I1R1 + I3R3; для рис.5 (один контур): U– E1+E2 =IR.
Мощность в электрической цепи (рис.6), отдаваемая источником (активный элемент с характеристикой E) P=E*I; мощность, потребляемая приёмником (пассивный элемент с параметром R) P2=I2R; потери мощности на внутреннем сопротивлении источника ΔP=I2R0. Уравнение баланса мощностей: EI=I2R+I2R0. При составлении уравнения баланса мощностей учитывают направления токов и ЭДС в активных элементах. Если направления тока в ветви и ЭДС совпадают, то EI принимают со знаком + (плюс) – элемент работает в режиме источника и отдаёт в цепь электрическую энергию. Если – противоположны, то со знаком – (минус) – источник ЭДС работает в режиме приёмника и потребляет электрическую энергию. Для электрической цепи (рис.3) уравнение баланса мощностей запишется
--E1I1+ E4I4+ E6I6=I12R1+ I22R2+ I32R1+ I42R4+ I52R5+ I62R6
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.