Проектирование принципиальной схемы процессора для вычисления функции cos(x) методом «цифра за цифрой», страница 2

где

Пределом последовательности на первом этапе является постоянная c, равная (в зависимости от типа вычисляемой функции) нулю или единицы. Результатом первого этапа является получение набора значений .

На втором этапе в качестве начального значения в зависимости от типа вычисляемой функции берутся нуль, единица либо некоторая константа, соответствующая данной функции. На основание полученного на первом этапе набора значений  строится итерационная последовательность, пределом которой служит значение вычисляемой функции.

Обозначим разность между k-м членом последовательности первого этапа и ее пределом [2]

                                                                                               (3)

Метод «цифра за цифрой» в контексте вычисления тригонометрических функций

Введем следующие обозначения:

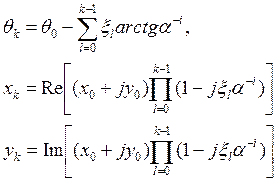                                                                (4)

где , , - начальные значения.

Запищим рекуррентные соотношения вычисления функций sin(phi), cos(phi):

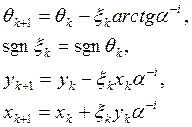                                                                                         (5)

Начальные значения: ,,

Конечные значения: ,,

Для синхронной организации (а организация нашего микропроцессора синхронная):

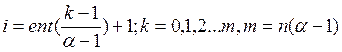
Значения K выбираются в соответствие с системой счисления  =2, а следовательно K = 1.646 [2]

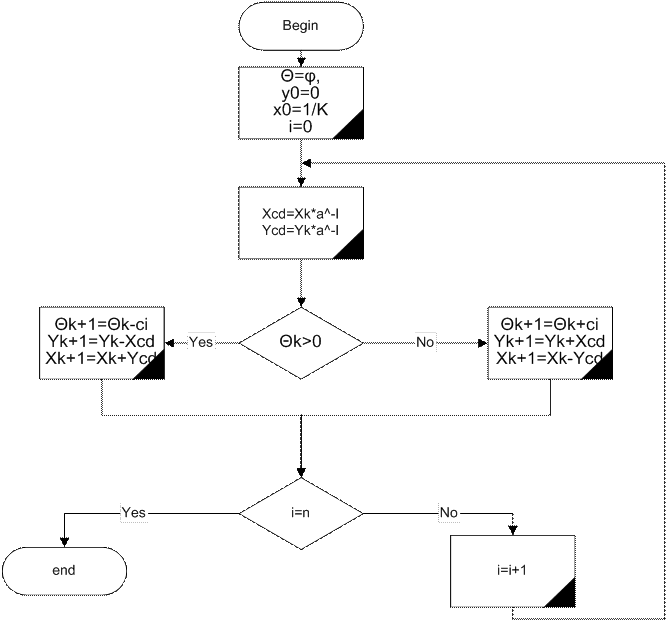
Рисунок 1

Замечание: Хочу отметить что алгоритм, изображенный на рис.1 не дополнен еще приведением аргумента. Эта часть алгоритма обсуждается в следующей главе пояснительной записки, где будет уже представлен полный алгоритм вычисления с учетом ситуации приведения (как требует задание).

Учет приведения аргумента в первую четверть

Поскольку аргументы элементарных функций могут изменяться в гораздо более широких приделах, чем допускается областью сходимости, то возникает необходимость в использовании формул привидения.

К общим вопросам умещения диапазона изменения аргументов элементарных функций относятся:

определение ограничений, накладываемых на аргументы и вызванных как естественным диапазоном изменения, так и рабочим диапазоном машинных чисел;

определение особых точек или областей (переполнение, запрещенные операции и т.п.)

Серьезным преимуществом метода «цифра за цифрой» является широкая область сходимости большинства элементарных функций, что в ряде случаев исключает необходимость приведения аргументов. Этой особенностью данный метод выгодно отличается от большинства численных методов, требующих для приведения аргументов большого объема вычислений, часто превышающего трудоемкость непосредственного вычисления функции.

Для периодических функции sin(phi), cos(phi) наиболее просто записываются формулы приведения. Если выделить целую часть I и остаток F от деления phi на pi/2, то:

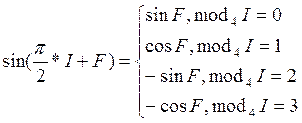                                                            (6)

Вычислим допустимые значения аргумента phi_доп по соотношению:

                                                              (7)

для =2 _доп =±1,743

Теперь дополним алгоритм вычисления косинуса приведением аргумента в первую четверть (или четвертую, если отрицательный аргумент). Полный алгоритм представлен на рисунке 2.

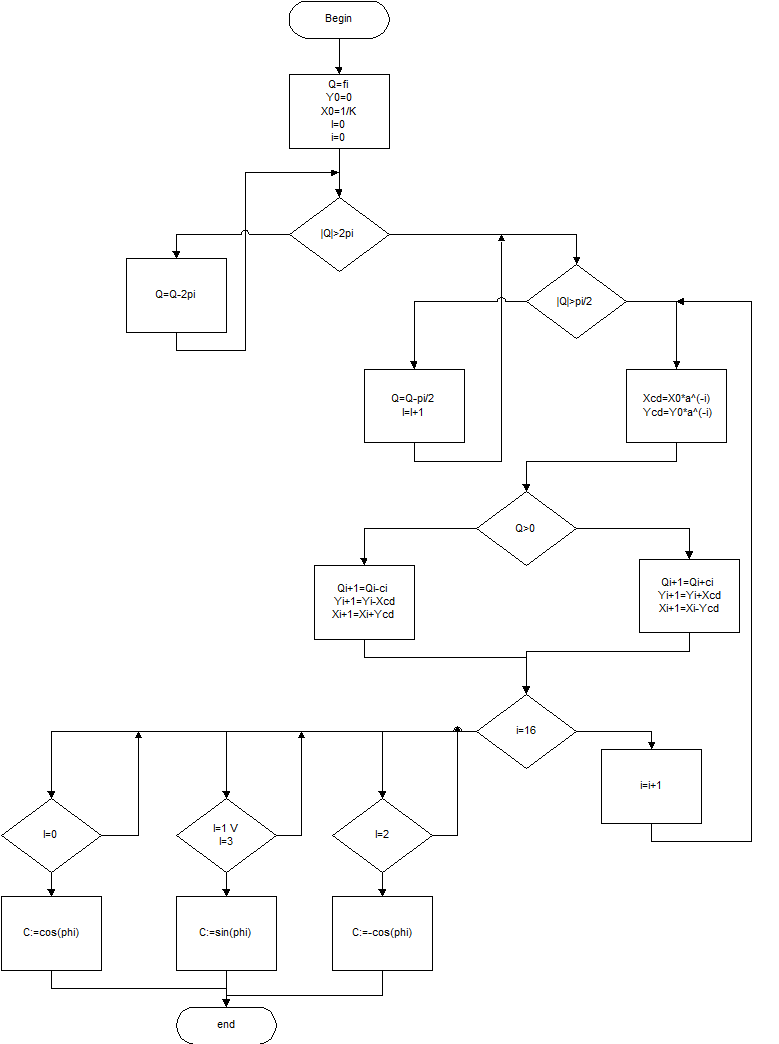
Рисунок 2

Проектирование основных узлов схемы

Выбор варианта реализации

Так в методе предусмотрено, что вычисление происходит с использованием констант , то разумно их поместить в ПЗУ. Констант будет 16, количество обусловлено количеством бит отведенных под число. В виду того, что из 16 констант последние 3 не помещаются в разрядную сетку, т.е. равны нулю, считаю разумным сделать разрядность шины 32 бита, вместо 16.Тем более в техническом задание строго не заданна разрядность шины. Кроме того, решиться проблема с суммированием маленьких и больших чисел, т.е. не придется использовать лишних сдвиговых регистров, что уменьшит временную стоимость алгоритма.

Необходимо в схеме будет использовать 3 типа регистров сдвиговые, буферные и хранящие (1533ИР13, 1533ИР22, 1517ИР1). Их необходимо расширить до разрядности 32 бита, так как стандартный регистр – 8 битный, кроме К1517ИР1, который уже 32 битный.