Проектирование принципиальной схемы процессора для вычисления функции cos(x) методом «цифра за цифрой»

ПОСТАНОВКА ЗАДАЧИ

Спроектировать принципиальную схему процессора для вычисления функции cos(x) методом «цифра за цифрой». Система счисления – двоичная. Диапазон существования аргумента – от –360 до 360 градусов. Разрядность результата – 16 бит. Особые требования – предусмотреть приведение аргумента в первую или четвертую четверть.

ВВЕДЕНИЕ

Микропроцессором называют построенное на одной или нескольких БИС программно – управляемое устройство, осуществляющие процесс обработки информации и управление им.

Микропроцессоры появились, когда интеграция БИС достигла уровня, при котором необходимые для программной реализации алгоритмов блоки удалось разместить на одном или нескольких кристаллах. Микропроцессор – центральный процессорный элемент микропроцессорной системы (или микро-ЭВМ), в состав которой входят также память и устройства ввода/вывода.

Совокупность микропроцессорных и других микросхем, совместимых по архитектуре, электрическим параметрам и конструктивному исполнению, т.е. пригодных для совместного применения, называется микропроцессорным комплектом БИС (МПК БИС). Понятие МПК задает номенклатуру микросхем с точки зрения возможностей их совместного применения. В состав МПК могут входить микросхемы различных серий и различных схемотехнических типов при условии их совместимости.

В МПС организуется процесс выполнения заданной программы, ее универсальность определяется тем, что самые разные задачи можно решать путем выполнения последовательности действий, входящих в систему команд. Таким образом, МПС это вычислительная, контрольно-измерительная или управляющая система, обрабатывающим элементом которой служит микропроцессор.

Основными типами существующих центральных процессорных элементов (т.е. собственно микропроцессоров) является однокристальные и многокристальные (секционные, наращиваемые).

Микропроцессоры, размещенные на оном кристалле, имеют фиксированные разрядность слова и систему команд. Многокристальные микропроцессоры составляются из нескольких малоразрядных секций (разрядность сечений – bit-slice). На одном кристалле при этом размещаются секция из малого числа разрядов и ее можно усложнить. Главные отличия многокристальных микропроцессоров – изменяемая разрядность слов (зависящая от числа связанных другом с другом секций) и возможность изменения микропрограмм, т.е. сменная система команд. Для изменения системы команд нужно изменить содержимое ПЗУ, хранящего микропрограммы.

Многокристальные (микропрограммируемые) микропроцессоры имеют большие вычислительные возможности, так как система команд у них может быть приспособлена к условиям решаемых задач, однако реализация собственной системы команд – относительно сложная задача. Однокристальные микропроцессоры проще в использовании и имеют широкое применение, где их возможности обеспечивают необходимую производительность системы [1]. В данной работе мы спроектируем однокристальный микропроцессор.

ОПИСАНИЕ МЕТОДА «ЦИФРА ЗА ЦИФРОЙ»

Как известно, итерационные процессы в общем виде заключаются в построении последовательности , сходящейся к функции U(x), где  - начальное приближение, а k=0,1,2…,k_max

Два соседних члена итерационной последовательности связанны соотношением:

                                                                                       (1)

где  - векторное поле, указывающее направление движение;  - положительный скаляр, показывающий длину шага итерации.

Выбор величин  имеет большое значение для сходимости итерационного процесса как таковой и для ее качественных характеристик – скорости, диапазона и т.д. Выбор величин , зависящих от разности между текущим членом последовательности и ее пределом или разности между двумя соседними членами, создает «обратную связь» между величиной невязки и шагом итерации и ускоряет сходимость. В то же время область сходимости при этом уменьшается. Выбор набора величин , заранее рассчитанный на «худший случай», расширяет диапазон сходимости, но часто увеличивает среднее число итераций при каждом конкретном значение аргумента.

Метод «цифра за цифрой» в первую очередь характеризуется тем, что изменение модуля шага итерации  происходит всякий раз только после получения очередной верной цифры результата. Минимально необходимое для этого число итерации либо определяется априорно для каждого типа функций, либо выбирается в процессе вычислений на основание признаков сходимости. Отсюда следует, что суммарное число итераций определенным образом связанно с количеством цифр, т.е. разрядностью операндов.

Во-вторых, указанное число итераций, определяемое условиями сходимости метода непосредственно зависит от основания используемой системы счисления.

Обобщая, можно сказать, что метод «цифра за цифрой» называется итерационный процесс, основные характеристики которого непосредственно зависят от основания используемой системы.

Техника применения метола состоит в разбиение процесса вычисления функции f(x) на 2 этапа. На обоих этапах строится итерационная последовательность вида (1), начальным значением которой на первом этапе служит величина аргумента функции, представленного n – разрядной правильной дробью:

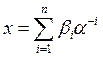                                                                                             (2)