Разработка и проектирование функциональной схемы процессора для вычисления функции sin(j) методом "цифра за цифрой", страница 2

Функции sin(j), cos(j).

Этап I 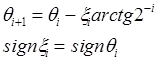                                            (1)     

Этап II 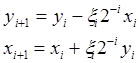                                              (2)      где i=0,1,2,...,n-1

Начальные условия: =j, =0,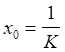

Результаты: , .

Коэффициент К (коэффициент деформации вектора) вычисляется перед началом использования рекурентных соотношений по формуле 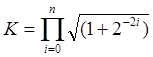(3)

                                             (3)     

1.2.Формулы приведения функции sin(j) в первую  четверть

Если выделить целую часть I и остаток F от деления j на p/2, то значение sin(j) определяется по формуле (4).

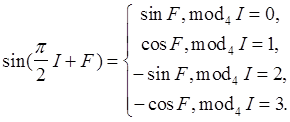                            (4)

	5

2. РАЗРАБОТКА АЛГОРИТМА И СОСТАВЛЕНИЕ БЛОК- СХЕМЫ

6

2.1. Блок-схема алгоритма вычисления функции sin(j) методом "цифра за цифрой"
2.2. Формат данных

Табл. 1

Разрядная сетка процессора n=24. Входным данным процессора является угол j, который может находиться в пределах ¸2p, поэтому формат входного данного (аргумента j) будет следующим: (Таблица 1)

биты
23	22	21	20	19	18	17	16	15	14	13	12	11	10	9	8	7	6	5	4	3	2	1	0
зн	целая часть			дробная часть

Табл. 2.

После вычисления значения функции разрядная сетка результата будет иметь вид представленный в таблице 2.

Биты
23	22	21	20	19	18	17	16	15	14	13	12	11	10	9	8	7	6	5	4	3	2	1	0
зн	целая часть	дробная часть

2.3. Контрольный пример

Табл. 3.

Вычисление контрольного  примера производилось с помощью ЭВМ. Для этого была написана программа  на алгоритмическом языке Турбо-Си (см. листинг программы в приложении). Аргумент j=0.785 находится в регистре Х, конечный результат находится в соответствии с алгоритмом в регистре Y.(Таблица 3.)

					i
01001101	01001101	00000000	00000000	01100100	0	01001101	10110011	00000000
01001101	00100110	10110011	11011001	00000000	1	00100110	10001101	11000101
00100110	00001001	10001101	11100011	11000101	2	01000011	10010110	11100100
01000011	00001000	10010110	11110010	11100100	3	01010001	10011110	11110011
01010001	00000101	10011110	11111001	11110011	4	01011000	10100011	11111010
01011000	00000010	10100011	11111101	11111010	5	01011011	10100101	11111101
01011011	00000001	10100101	11111110	11111101	6	01011101	10100110	11111110

Как видно из приведенной выше таблицы sin(j)=01011010 ( в соответствии с алгоритмом в Y находится значение -sin(j) ), что совпадает со значением посчитанным на калькуляторе: sin(j)=01011010.