Методическая погрешность полиномиальной аппроксимации знакопеременна и равномерно распределена по промежутку изменения аргумента. К недостаткам этого метода следует отнести большую загрузку ПЗУ, в котором должны быть записаны коэффициенты всех аппроксимирующих полиномов. Преимуществом цепных дробей является малый требуемый объем ПЗУ, принципиально более широкая область сходимости, чем для ряда Тейлора, и универсальность применения программы (микропрограммы) вычисления цепной дроби для различных функций. Недостатком метода является, во-первых, необходимость наличия в системе команд процессора операции деления, во-вторых, большое время вычисления, которое даже для самого быстрого способа составляет равно tц.др.=n(tумн+tдл+tсл), где n – число звеньев дроби, зависящее от вида функции и требуемой точности, tц.др.- время реализации цепных дробей.
При использовании рациональных приближений элементарные функции представляются в виде отношения двух полиномов с числом членов в каждом, намного меньшим, чем для соответствующих разложений в ряд Тейлора. Однако при данном методе все коэффициенты полиномов предварительно должны быть занесены в память. Время вычисления элементарной функции при использовании элементарных приближений складывается из времени вычисления двух полиномов и операции выполнения деления.
Сущность итерационных методов состоит в построении последовательности yi+1=f(yi), сходящейся к y(x). Эффективность применения этих методов зависит, во-первых, от скорости сходимости (необходимого числа итераций от заданной точности), и, во-вторых, от набора операций выполняемых на каждом шаге.
Различные табличные методы основаны на кусочно-линейной или криволинейной аппроксимации. Достоинством этих методов является малое требуемое число арифметических операций, необходимое для вычисления функций. Однако для таких методов характерно применение больших объемов памяти. Этот фактор ограничивает практическое применение этого метода.
Из всех рассмотренных выше методов при реализации на ЦЭВМ наиболее часто используется метод полиномиальной аппроксимации.
Однако в последнее время внимание разработчиков вычислительных машин стал привлекать один итерационный метод, который может быть отнесен к методам “цифра за цифрой”. Надо отметить, что к этим методам относят любой процесс вычисления, в результате выполнения которого получают одну надежную цифру результата.
Вычисление любой элементарной функции по этому методу сводится к выполнению двух этапов.
На первом этапе аргументы элементарных функций, заданные n-разрядными кодами в позиционной системе счисления с основанием а и являющиеся правильными дробями представляются либо сходящимся произведением, либо суммой n слагаемых одного из следующих видов:
ln(1+Ei *a-i) ;
Ei *arctg(a-i);
Ei *arth(a-i);
Искомым на данном этапе является набор операторов Ei, для которых могут быть выбраны два рода значений: 0 и1 или +1 и –1. В первом случае говорят о итерационном процессе со знакопостоянными, а во втором со знакопеременными шагами. На втором этапе на основании найденного в предыдущем этапе набора значений операторов Ei определяется величина искомой функции. Это выполняется суммированием слагаемых одного их видов:
ln(1+Ei *a-i) ;
Ei *arctg(a-i);
Ei *arth(a-i);
Каждый этап выполнения выполняется за n шагов и представляет собой процесс, состоящий в последовательности: ui=f(ui-1). Для проведения двух указанных этапов необходимо выполнение двух типов операции: алгебраического сложения и сдвига.
Описание алгоритма
Алгоритм
При рассмотрении рекуррентных соотношений вычисления функции log2 x
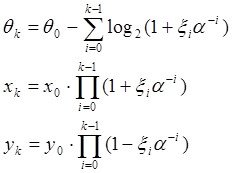
где
, x0 , y0 –
начальные значения итерационных последовательностей.
Получим рекуррентные соотношения собственно для вычисления функции log2 x:
yk+1=
xk+1=
sign(
)=sign (yk)
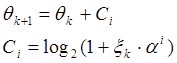
При
этом начальные значения: x0=X, y0=1 –X, 
=0. Конечные значения: : xкон=1,
yкон=0, 
=-log 2x.
В
случае синхронной организации i=ent(k
/
)+1,k=0,1,2…,m;
m=n
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.