

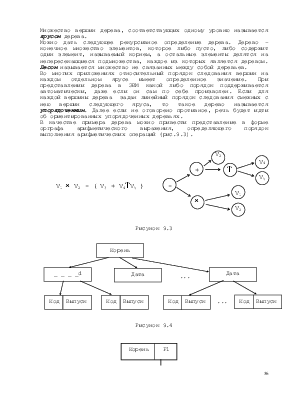
В предыдущих лекциях мы рассматривали линейные списки и их хорошо формализованное описание в терминах отношений реляционной модели данных. Каждый список отражает в основном отношение физического соседства в каком либо аспекте. В то же время в предметных областях присутствуют отношения подчинения, отношение вхождения, отношения причинной обусловленности и ряд других отношений, которые требуют использования для своего описания нелинейных структур данных. На рис.9.1 представлены отношения взаимообусловленности этапов изучения и контроля знаний по учебной дисциплине, которые передаются с помощью нелинейной структуры.
 |
![]()
![]()
![]()

 Своевременность нет
Своевременность нет
![]()
|
|
Рисунок 9.1
В данном случае требуется сетевая структура данных, логическая концепция которой опирается на общее математическое понятие графа. Очевидно, что программная реализация такого рода структур требует специфических приемов и методов. Ниже изучение нелинейных структур будет идти в следующем порядке:
- математическое описание объектов типа дерева и графа и свойств этих объектов,
- структуры данных типа дерева и графа,
- способы хранения нелинейных структур и манипулирования ими.
Граф G включает некоторое множество V вершин графа, множество E, называемое множеством ребер графа, и отображение G множества ребер Е графа на множество пар элементов декартова произведения Vx V. В качестве синонима для термина «вершина» будет использоваться слово «узел». Везде далее будет считаться, что множества Е и V конечны. Граф обозначается следующим образом:
G
Е ------а (V x V).
Из определения следует, что каждому ребру графа ставится в соответствие пара вершин этого графа. Если ребру е из Е сопоставлена пара вершин (u,v), где u и v принадлежат V., то будем говорить, что ребро е соединяет вершины u и v, и эти вершины называются смежными. Если порядок вершин, соответствующих ребру е важен, то е – ориентированное ребро, в противном случае ребро называется неориентированным.
Это позволяет ввести следующую классификацию графов:
- ориетированные графы (орграфы),
- неориентированные графы,
- смешанные графы.
К последней группе относятся графы, для которых одновременно не пусты множество ориентированных ребер и множество неориентированнных ребер. Для ориентированного ребра существует понятие начальной и конечной вершины.
Простой орграф соответствует ситуации, когда между любой парой вершин имеется не более одного ребра данного направления. Вообще говоря, простой орграф можно отобразить с помощью матрицы смежности (матрицы инциденций (рис.9.2). Для этого необходимо установить взаимно-однозначное соответствие между N вершинами орграфа и целыми числами от единицы до N (пронумеровать вершины графа). В этом случае элемент матрицы смежности на пересечении строки i и столбца j равен единице в том и только в том случае, если вершина i и j являются соответственно начальной и конечной вершинами ребра графа, и равен нулю в противном случае.
![]()
![]()
![]() B D A B C
D
B D A B C
D
![]()

 A æ 0 1 1 0 ö
A æ 0 1 1 0 ö
B ç 0 0 1 1 ÷
![]()
![]() C ç 0 0 0 1 ÷
C ç 0 0 0 1 ÷
![]() A C D è 0 0 0 0 ø
A C D è 0 0 0 0 ø
Рисунок 9.2
Полустепень исхода – число ребер, исходящих из данной вершины; полустепень захода – число ребер, для которых данная вершина является конечной. Степень вершины определяется суммой полустепени исхода и полустепени захода.
Последовательность ребер простого орграфа, для которых конечная вершина любого ребра кроме последнего является начальной вершиной следующего ребра, задает путь в графе. Число ребер в этой последовательности называется длиной пути. Простой путь – путь, все ребра в котором различны. Элементарный путь – путь в котором различны все вершины.
?? Можно показать, что все элементарные пути являются простыми.
Путь, начинающийся и заканчивающийся в одной и той же вершине, называется циклом (контуром).
Ациклический граф – простой орграф, не имеющий ни одного цикла.
Ориентированное дерево – это ациклический орграф, у которого одна из вершин (корень) имеет полустепень захода ноль, а остальные – полустепени захода, равные единице.
Лист дерева – вершина с нулевой полустепенью исхода. Уровень вершины дерева определяется длиной пути от корня до этой вершины. Множество вершин дерева, соответствующих одному уровню называется ярусом дерева.
Можно дать следующее рекурсивное определение дерева. Дерево – конечное множество элементов, которое либо пусто, либо содержит один элемент, называемый корнем, а остальные элементы делятся на непересекающиеся подмножества, каждое из которых является деревом. Лесом называется множество не связанных между собой деревьев.
Во многих приложениях относительный порядок следования вершин на каждом отдельном ярусе имеет определенное значение. При представлении дерева в ЭВМ какой либо порядок поддерживается автоматически, даже если он сам по себе произволен. Если для каждой вершины дерева задан линейный порядок следования смежных с нею вершин следующего яруса, то такое дерево называется упорядоченным. Далее если не оговорено противное, речь будет идти об ориентированных упорядоченных деревьях.
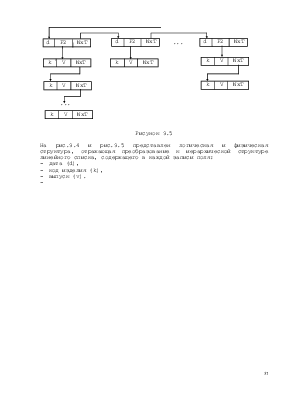
В качестве примера дерева можно привести представление в форме орграфа арифметического выражения, определяющего порядок выполнения арифметических операций (рис.9.3).
![]()
![]() V2
V2
![]()
![]()
![]()
![]() V4
V4
![]()
![]()
![]() +
+
![]()
![]() V5
V5
![]()
![]() V1 ´ V2 -
( V3 + V4V5 )
V1 ´ V2 -
( V3 + V4V5 ) ![]()
![]() V1
V1
![]()
![]() ´
´
V2
Рисунок 9.3
 |
...
 |
|||||
 |
 |
||||
...
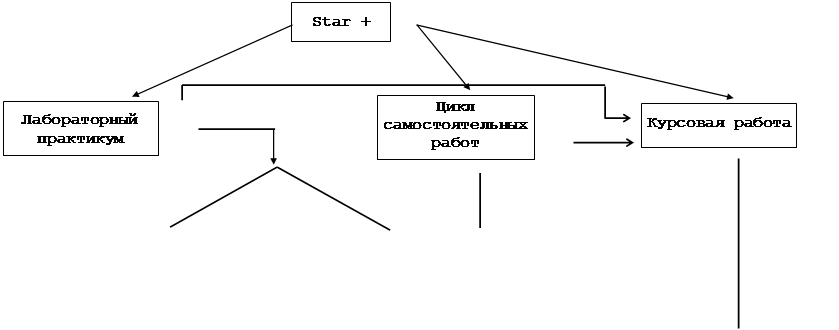
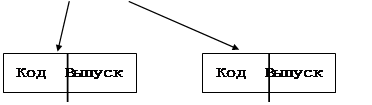
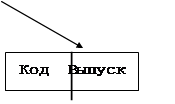
Рисунок 9.4
 |
...
 |
|||||
 |
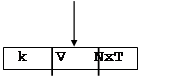 |
||||
![]()
![]()
|
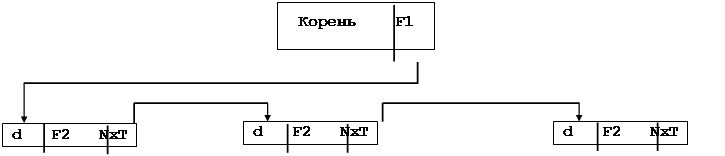
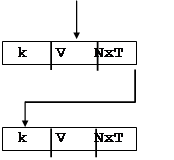
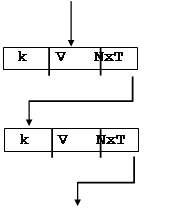
Рисунок 9.5
На рис.9.4 и рис.9.5 представлен логическая и физическая структура, отражающая преобразование к иерархической структуре линейного списка, содержащего в каждой записи поля:
- дата (d),
- код изделия (k),
- выпуск (v).
-
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.