Сбалансированные бинарные деревья. Включение вершины в сбалансированное дерево поиска

Лекция 12. Сбалансированные бинарные деревья.

Дерево называется идеально сбалансированным, если для каждой его вершины число вершин в её левом и правом поддереве отличается не более, чем на единицу.

Пусть требуется построить идеально сбалансированное дерево для записей, поступающих из входного файла. Это дерево будет отличаться минимальной глубиной, которая определяется максимальным уровнем листьев дерева. При этом будем считать глубину пустого дерева равной –1. Очевидно минимальная глубина при заданном числе вершин дерева достигается, если на всех уровнях кроме последнего помещать максимальное число вершин. Для бинарного дерева это означает, что приходящие вершины нужно размещать поровну слева и справа от каждой вершины. Правило такого распределения для известного числа n лучше сформулировать, используя рекурсию:

-  взять одну вершину в качестве корня;

-  построить тем же способом левое поддерево с n1 вершинами, где ;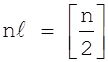

-  построить тем же способом правое поддерево с n2 вершинами, где .

Блок-схема соответствующего алгоритма представлена на рис.1.

                             да

   Начало         n = 0              p = N/L            return p

 

нет

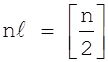                            Ввод Х         p^.rp:= maketree(nr)

           

 

                 new (p)           p^.inf = x       p^.lp:= maketree(nl)

Рисунок 1.

Однако использовать полученное дерево как высокоорганизованную структуру с практической целью невозможно по двум причинам:

-  приведенный выше алгоритм построения не учитывает содержание информационной части вершин дерева;

-  не найдено эффективных алгоритмов построения и модификации идеально сбалансированных деревьев с учетом информационной составляющей вершин дерева.

Более полезным в этом плане является класс сбалансированных бинарных деревьев.

Дерево называется сбалансированным тогда и только тогда, когда для каждой его вершины глубины её левого и правого поддерева различаются не более, чем на единицу.

Это определение приводит к простым процедурам его формирования и модификации при том, что время поиска в таких деревьях пропорционально логарифму n по основанию 2. То есть за такое время можно:

-  найти вершину с заданным ключом;

-  включить в дерево вершину с заданным ключом;

-  исключить вершину с заданным ключом.

Это является следствием доказанной Адельсоном-Вельским Г.М. и Ландисом Е.М. теоремы, гарантирующей, что глубина сбалансированного дерева никогда не будет превышать глубину идеально сбалансированного дерева более, чем на 45%.

Включение вершины в сбалансированное дерево поиска.

Если у нас есть корень R , левое поддерево А и правое поддерево B, то необходимо различать три возможных случая. Пусть включение в А новой вершины приведет к увеличению на единицу его глубины. Тогда возможно три случая:

-  глубины деревьев А и В были одинаковы, после модификации глубины перестанут совпадать, но критерий сбалансированности не нарушится;

-  глубина дерева А была меньше глубины дерева В, после модификации критерий сбалансированности не нарушится;

-  глубина дерева А превышала глубину дерева В, после модификации получится не сбалансированное дерево.

Проиллюстрируем последний случай на дереве поиска, сконструированном из массива целых чисел:

8,4,10,2,6.

Добавление к дереву одного из ключей 1,3,5,7 после традиционной процедуры включения вершины в дерево потребует дополнительной балансировки (см. рис.2).Из рисунка 3 видно, что существуют два качественно различных случая для выполнения процедуры балансировки:

-  нарушение возникает из-за левого поддерева дерева А;

-  нарушение возникает из-за правого поддерева дерева А.

                      8

4                10

 

2        6

Рисунок.2.

а)               8                              4

           4         10          Þ        2             8

      2       6                      1             6            10

1

б)               8                                4

           4          10         Þ       2                 8

2          6                              3      6          10