Методы линейного построения массивов Suffix Array, страница 2

1.  Строим массив суффиксов из суффиксов, начинающихся на позициях i mod 3≠0. Это можно сделать при помощи рекурсивной сортировки двух третей исходной строки.

2.  Отсортируем остающиеся суффиксы, используя информацию, полученную в шаге один.

3.  Соединяем две отсортированных последовательности, полученные в шагах один и два.

Использование двух третей вместо половины суффиксов в первом шаге делает последний шаг почти тривиальным: простое слияние на основе сравнения достаточно. Например, чтобы сравнить суффиксы, начинающиеся в i и j с i mod 3=0 и j mod 3 = 1, мы сначала сравниваем начальные символы, и если они те же самые, мы сравниваем суффиксы, начинающиеся с позиций  i+1 и j + 1, чей относительный порядок уже известен из первого шага.

Простота искажающегося алгоритма облегчает адаптацию к другим моделям вычислений.

Еще один алгоритм построения массива суффиксов в линейное время был предложен Pang Ko and Srinivas Aluru. Рассмотрим его более подробно.

Алгоритм построения массива SA в линейное время

Рассмотрим строку состоящую из алфавита ∑ ={1…n}. Без потери общности, примем, что последний символ строки Т не содержится более нигде в Т и он является самым минимальным лексикографическим символом. Обозначим его символом «$». Обозначим каждый i-тый суффикс номером согласно его номера первого символа. Обозначим   суффикс согласно его стартового номера символа . Для хранения суффикса , будем использовать только его стартовый номер i. Классифицируем все суффиксы по двум типам L и  S. Примем, что суффикс  является типом S, если  и этот суффикс типа L, если .

Важная собственность типов S и  L суффиксов, если суффикс типа S или типа L оба начинается с одного и того же самого символа, тип суффикса  S всегда лексикографически больше чем тип L.

Пусть А будет массивом содержащим все суффиксы строки Т, не обязательно в отсортированном порядке. Пусть B будет массивом, содержащим все суффиксы S типа строки Т, отсортированные в лексикографическом порядке. Используя массив В, мы сможем вычислить лексикографический порядок всех оставшихся суффиксов в массиве А. Для этого надо сделать следующее:

1.  Все суффиксы строки Т разобьем на группы согласно их первому символу в массиве А. Каждая группа будет содержать все суффиксы, которые начинаются с одного и того же символа. На этот шаг требуется O(n) time.

2.  Просматривая В с права на лево, для каждого символа встретившегося в просмотре, перенесем этот суффикс в текущий конец его группы и передвинем указатель конца группы на одну позицию влево.  Под перемещением суффикса в массиве А на его новую позицию понимается перемена мест этого суффикса с суффиксом в новой позиции. После выполнения этого этапа все суффиксы S типа будут находиться в корректных позициях в массиве А. Время выполнения этого, этапа  которое не превышает O(n).

3.  Сканируя массив А слева направо, для каждого вхождения А[i] если  является суффиксом L типа, то перемещаем его в текущее начало группы и передвигаем указатель начала группы вправо на одну позицию. Этот этап выполняется также в O(n) time. Результатом выполнения этого алгоритма будет получен массив SA в линейное время.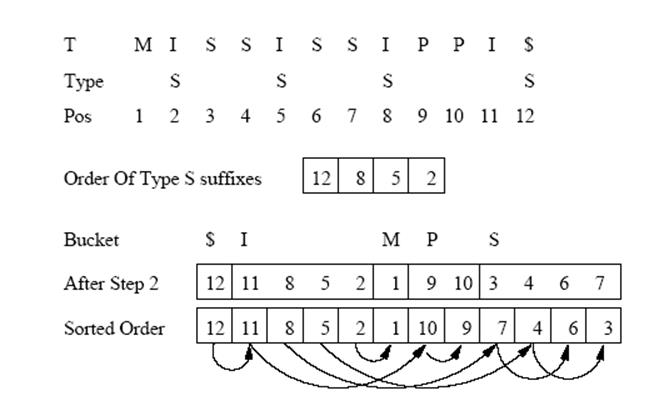

Покажем как можно получить массив В отсортированный в лексикографическом порядке.

Наша цель это сортировать все суффиксы S типа строки Т. Для выполнения этой процедуры мы сортируем все подстроки S типа. Сортировка выполняется группами где все подстроки в группе идентичны. Группы нумеруются используя последовательные целые числа начиная с 1. Создаем новую строку  по следующему правилу: просматривая строку Т слева направо и для каждой позиции S типа, запишем номер группы подстроки S типа с которой она начинается.  Эта строка является номером группы формы . Замечая что каждый суффикс S типа в строке Т естественным образом передается суффиксом в новой строке  .

В начале мы покажем, как сортируются все подстроки S типа в O(n). Рассмотрим массив А, содержащий все суффиксы строки Т, сгруппированные согласно их первому символу. Для каждого  суффикса определим его S-distance, являющеюся расстоянием от его стартовой позиции i до ближайшей позиции S типа находящейся слева от i (исключая позицию i). Если слева не содержится  ни одной позиции S типа, то S-distance равен 0. Таким образом, для каждого суффикса начинающего на или после первой позиции S типа в строке Т, его расстояние S-distance равно 0. Массив В будет отсортирован по следующему алгоритму:

1.  Для каждого суффикса в массиве А, определим его S-distance. Это будет выполнено при просмотре строки Т слева направо, сохранением дорожки расстояния из текущей позиции до ближайшей позиции S типа слева.  Пока мы в позиции i, расстояние до ближайшей позиции S типа слева  известно и его необходимо сохранить в массиве Dist. Расстояние S-distance суффикса  хранится в массиве Dist[i]. Следовательно, S-distance может всех суффиксов может быть записан в линейное время.

2.  Пусть m будет максимальным расстоянием S-distance. Создадим список m такой что список j  (удовлетворяет условию 1<j<m) будет содержать все суффиксы с S-distance, в том порядке в каком они появляются в массиве А. Это может быть сделано при помощи просмотра массива А слева направо в линейное время, обращаясь к Dist [А[i]], чтобы поместить  в правильный список.

3.  Теперь отсортируем подстроки S типа используя список созданный выше. Сортировка будет выполнятся при помощи повторения групп использую один символ за раз. Начнем с группировки основанных на первых символах определяемые порядком в котором  суффиксы S типа появляются в массиве А. Предположим что подстроки S типа группируются согласно их первому j-1 символу. Расширив это на все j символы, мы сканируем список j. Для каждого суффикса встретившегося в просмотре переместим подстроку S типа  в текущее начало её группы. Так как суммарный размер всех списков O(n), значит сортировка подстрок S типа так же уложится в O(n).